Решение: В координатах давление-объем график процесса в идеальном одноатомном газе имеет

Условие задачи:

В координатах давление-объем график процесса в идеальном одноатомном газе имеет вид прямой, соединяющей точки (0,8 л; 100 кПа) и (1 л; 80 кПа). Определить изменение внутренней энергии газа в ходе процесса. Масса газа постоянна.

Задача №5.4.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V_1=0,8\) л, \(p_1=100\) кПа, \(V_2=1\) л, \(p_2=80\) кПа, \(m=const\), \(\Delta U-?\)

Решение задачи:

Всем известно, что изменение внутренней энергии \(\Delta U\) одноатомного идеального газа можно определять по формуле:

\[\Delta U = \frac{3}{2}\frac{m}{M}R\left( {{T_2} – {T_1}} \right)\]

Перепишем формулу в таком эквивалентном виде:

\[\Delta U = \frac{3}{2}\left( {\frac{m}{M}R{T_2} – \frac{m}{M}R{T_1}} \right)\;\;\;\;(1)\]

Запишем уравнение Клапейрона-Менделеева для точек с объемами и давлениями, указанными в условии:

\[\left\{ \begin{gathered}
{p_1}{V_1} = \frac{m}{M}R{T_1} \hfill \\
{p_2}{V_2} = \frac{m}{M}R{T_2} \hfill \\
\end{gathered} \right.\]

Тогда формула (1) примет вид:

\[\Delta U = \frac{3}{2}\left( {{p_2}{V_2} – {p_1}{V_1}} \right)\]

Задача решена в общем виде. Переведём объемы газа в систему СИ:

\[0,8\;л = 0,8 \cdot {10^{ – 3}}\;м^3\]

\[1\;л = 1 \cdot {10^{ – 3}}\;м^3\]

Произведём вычисления:

\[\Delta U = \frac{3}{2}\left( {80 \cdot {{10}^3} \cdot 1 \cdot {{10}^{ – 3}} – 100 \cdot {{10}^3} \cdot 0,8 \cdot {{10}^{ – 3}}} \right) = 0\;Дж\]

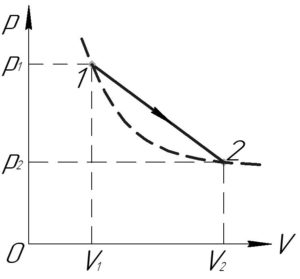
Так как мы получили нулевое изменение внутренней энергии, значит \({p_1}{V_1}={p_2}{V_2}\). По закону Бойля-Мариотта это значит, что эти указанные точки лежат на изотерме (штриховая толстая линия на схеме).