Решение: В ведре находится смесь воды со льдом массой m=10 кг. Ведро внесли в комнату

Условие задачи:

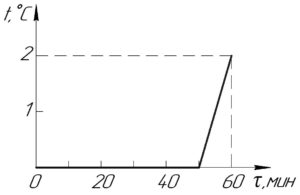В ведре находится смесь воды со льдом массой \(m=10\) кг. Ведро внесли в комнату и сразу же начали измерять температуру смеси. Получившаяся зависимость температуры смеси от времени изображена на рисунке. Определить массу льда в ведре в момент внесения его в комнату.

Задача №5.2.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) кг, \(\Delta m-?\)

Решение задачи:

Время плавления льда в смеси \(\tau_1\) равно 50 мин, время нагревания воды \(\tau_2\) равно 10 мин, температура \(t_1\) равна 0 °C, температура \(t_2\) равна 2 °C (смотрите схему).

Чтобы расплавить лёд массой \(\Delta m\), содержащийся в смеси, нужно количество теплоты \(Q_1\), которое можно определить по формуле:

\[{Q_1} = \lambda \Delta m\;\;\;\;(1)\]

Удельная теплота плавления льда \(\lambda\) равна 330 кДж/кг.

Для нагревания воды массой \(m\) (после расплавления льда) от температуры \(t_1\) до температуры \(t_2\) необходимо количество теплоты \(Q_2\), определяемое по формуле:

\[{Q_2} = cm\left( {{t_2} – {t_1}} \right)\;\;\;\;(2)\]

Удельная теплоёмкость воды \(c\) равна 4200 Дж/(кг·°C).

Вообще, смесь воды со льдом будет нагреваться, поскольку будет происходить теплообмен с воздухом комнаты. При этом нет причин полагать, что подводимая тепловая мощность \(N\) (от воздуха комнаты) меняется со временем. Так как количество теплоты равно произведению тепловой мощности на время, то можно получить такую систему:

\[\left\{ \begin{gathered}
{Q_1} = N{\tau _1} \hfill \\
{Q_2} = N{\tau _2} \hfill \\
\end{gathered} \right.\]

Учитывая формулы (1) и (2), система примет вид:

\[\left\{ \begin{gathered}
N{\tau _1} = \lambda \Delta m \hfill \\
N{\tau _2} = cm\left( {{t_2} – {t_1}} \right) \hfill \\
\end{gathered} \right.\]

Поделим нижнее равенство на верхнее, тогда:

\[\frac{{\lambda \Delta m}}{{cm\left( {{t_2} – {t_1}} \right)}} = \frac{{{\tau _1}}}{{{\tau _2}}}\]

\[\Delta m = \frac{{cm\left( {{t_2} – {t_1}} \right){\tau _1}}}{{\lambda {\tau _2}}}\]

Переведём время \(\tau_1\) и \(\tau_2\) в систему СИ:

\[50\;мин = 3000\;с\]

\[10\;мин = 600\;с\]

Произведём вычисления:

\[\Delta m = \frac{{4200 \cdot 10 \cdot \left( {2 – 0} \right) \cdot 3000}}{{330 \cdot {{10}^3} \cdot 600}} = 1,27\;кг\]