Условие задачи:
Точечные положительные заряды \(q\) и \(2q\) закреплены на расстоянии \(L\) друг от друга в вакууме. На середине прямой, соединяющей заряды, поместили точечный отрицательный заряд \(-q\). Найти изменение модуля и направления силы, действующей на положительный заряд \(q\)?
Задача №6.1.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q\), \(2q\), \(L\), \(-q\), \(\frac{F}{F_0}-?\)
Решение задачи:
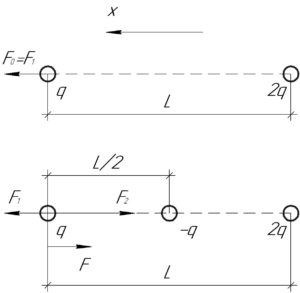 Вначале на заряд \(q\) действует лишь одна сила \(F_1\) (со стороны заряда \(2q\)), которую можно найти из закона Кулона по такой формуле:
Вначале на заряд \(q\) действует лишь одна сила \(F_1\) (со стороны заряда \(2q\)), которую можно найти из закона Кулона по такой формуле:
\[{F_1} = \frac{{2k{q^2}}}{{{L^2}}}\]
Так как на заряд \(q\) действует лишь одна сила, то результирующая сила \(F_0\) равна:
\[{F_0} = \frac{{2k{q^2}}}{{{L^2}}}\]
После того как на середине прямой, соединяющей заряды, поместят ещё один заряд \(-q\), на заряд \(q\) станет действовать ещё одна сила \(F_2\), модуль которой равен:
\[{F_2} = \frac{{4k{q^2}}}{{{L^2}}}\]
Так как \({F_2} > {F_1}\), то результирующая сила \(F\) согласно принципу суперпозиции равна:
\[F = {F_1} — {F_2}\]
\[F = \frac{{2k{q^2}}}{{{L^2}}} — \frac{{4k{q^2}}}{{{L^2}}}\]
\[F = \frac{{-2k{q^2}}}{{{L^2}}}\]
Знак «минус» показывает, что проекция силы \(F\) на ось \(x\) отрицательна. Найдём искомое отношение \(\frac{F}{F_0}\):
\[\frac{F}{{{F_0}}} = \frac{{ — 2k{q^2} \cdot {L^2}}}{{{L^2} \cdot 2k{q^2}}} = — 1\]
Получается, что сила изменила своё направление, а по модулю осталась той же величины.
Ответ: -1.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.1.28 Два одинаковых шарика, имеющих одинаковые заряды 1,6 мкКл, подвешены на одной
6.1.30 Точечные положительные заряды q и 2q закреплены на расстоянии L друг
6.1.31 Два маленьких одинаковых металлических шарика заряжены положительным зарядом 5q

 icodepro.ru
icodepro.ru