Условие задачи:
Точечный источник света находится на дне сосуда с жидкостью с показателем преломления 1,8. Во сколько раз максимальное время прохождения света до выхода в воздух больше минимального?
Задача №10.4.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(n=1,8\), \(\frac{t_2}{t_1}-?\)
Решение задачи:
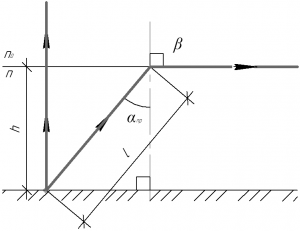 Если свет движется перпендикулярно дну сосуда, то он проходит минимальное расстояние, равное глубине сосуда \(h\), а значит затрачивает на это минимальное время, которое можно найти по следующей формуле (здесь \(\upsilon\) — скорость света в воде):
Если свет движется перпендикулярно дну сосуда, то он проходит минимальное расстояние, равное глубине сосуда \(h\), а значит затрачивает на это минимальное время, которое можно найти по следующей формуле (здесь \(\upsilon\) — скорость света в воде):
\[{t_1} = \frac{h}{\upsilon }\]
Свет пройдет в воде максимальное расстояние, если будет падать на поверхность воды под углом \(\alpha_{пр}\), то есть под углом полного внутреннего отражения. Световые лучи, падающие под большим углом, выходить из воды уже не будут. При этом время движения такого светового луча \(t_2\) можно найти по аналогичной формуле:
\[{t_2} = \frac{l}{\upsilon }\]
Из прямоугольного треугольника следует, что:
\[l = \frac{h}{{\cos {\alpha _{пр}}}}\]
Запишем закон преломления света (также известен как закон преломления Снеллиуса) для случая полного внутреннего отражения при переходе светового луча из воды в воздух:
\[n\sin \alpha_{пр} = {n_0}\sin {\beta}\]
Здесь \(\alpha_{пр}\) — предельный угол полного внутреннего отражения, \(\beta\) — угол преломления, равный в данном случае 90°, \(n\) и \(n_0\) — показатели преломления сред. Показатель преломления воздуха \(n_0\) равен 1, показатель преломления жидкости \(n\) равен 1,8. Так как \(n_0=1\) и \(\sin \beta_0 = 1\), то:
\[n\sin {\alpha _{пр}} = 1\]
\[\sin {\alpha _{пр}} = \frac{1}{n}\]
\[{\alpha _{пр}} = \arcsin \left( {\frac{1}{n}} \right)\]
Тогда:
\[l = \frac{h}{{\cos \left( {\arcsin \left( {\frac{1}{n}} \right)} \right)}}\]
Значит:
\[{t_2} = \frac{h}{{\upsilon \cos \left( {\arcsin \left( {\frac{1}{n}} \right)} \right)}}\]
Искомое отношение времен равно:
\[\frac{{{t_2}}}{{{t_1}}} = \frac{1}{{\cos \left( {\arcsin \left( {\frac{1}{n}} \right)} \right)}}\]
Задача решена, подставим данные задачи в полученную формулу и посчитаем численный ответ:
\[\frac{{{t_2}}}{{{t_1}}} = \frac{1}{{\cos \left( {\arcsin \left( {\frac{1}{{1,8}}} \right)} \right)}} = 1,2\]
Ответ: 1,2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.4.13 На дне сосуда, заполненного водой до высоты 0,40 м, находится точечный источник света
10.4.15 Преломляющий угол трехгранной призмы равен 60°. Найти угол падения луча света
10.4.16 В водоем на некоторую глубину помещают источник белого света. Показатели преломления

 icodepro.ru
icodepro.ru
Нужен ли нам показатель преломления воды, если у нас имеется другой показатель преломления жидкости?
Да конечно не нужен, решение исправлено