Условие задачи:
Точка движется по окружности с постоянной по величине скоростью 50 см/с. Вектор скорости изменяет направление на 90° за 2 с. Каково центростремительное ускорение точки?
Задача №1.8.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon=50\) см/с, \(\alpha=90^\circ\), \(t=2\) с, \(a_ц-?\)
Решение задачи:
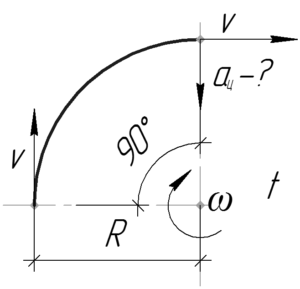 Начнем решать задачу с конца. Центростремительное ускорение точки \(a_ц\) можно найти по формуле:
Начнем решать задачу с конца. Центростремительное ускорение точки \(a_ц\) можно найти по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]
По формуле видно, что нам нужно узнать радиус окружности \(R\). Из каких соображений это можно сделать? Если вектор скорости изменил своё направление на 90°, значит точка прошла по окружности путь \(S\), равный четверти её длины. Длина окружности равна \(2\pi R\), поэтому:
\[S = \frac{{2\pi R}}{4} = \frac{{\pi R}}{2}\]
Так как движение точки по окружности является равномерным со скоростью \(\upsilon\), то:
\[\upsilon = \frac{S}{t} = \frac{{\pi R}}{{2t}}\]
Выразим из этой формулы нужный нам радиус \(R\):
\[R = \frac{{2\upsilon t}}{\pi }\]
В итоге формула для определения центростремительного ускорения такая:
\[{a_ц} = \frac{{{\upsilon ^2} \cdot \pi }}{{2\upsilon t}} = \frac{{\upsilon \pi }}{{2t}}\]
Переведем скорость точки из см/с в м/с.
\[50\; см/с = \frac{{50}}{{100}}\; м/с = 0,5\; м/с\]
Численно искомое ускорение равно:
\[{a_ц} = \frac{{0,5 \cdot 3,14}}{{2 \cdot 2}} = 0,39\; м/с^2\]
Ответ: 0,39 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.28 Колесо, имеющее 12 равноотстоящих спиц, во время вращения фотографируют
1.8.30 С какой скоростью будет перемещаться ось катушки, если конец нити тянуть
1.8.31 Стержень длиной 50 см вращается с частотой 30 об/мин вокруг перпендикулярной

 icodepro.ru
icodepro.ru