icodepro.ruУсловие задачи:
Точка движется равноускоренно. За 4 с она проходит путь 24 м. За следующие 4 с она проходит путь 64 м. Определить начальную скорость.
Задача №1.3.40 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=24\) м, \(S_2=64\) м, \(\upsilon_0-?\)
Решение задачи:
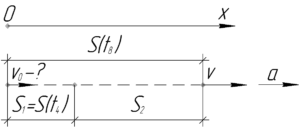Уравнение равноускоренного движения тела выглядит так:
\[S\left( t \right) = {\upsilon _0}t + \frac{{a{t^2}}}{2}\]
Путь \(S_1\) за первые \(t_4=4\) секунды запишем таким образом:
\[{S_1} = S\left( {{t_4}} \right)\]
\[{S_1} = {\upsilon _0}{t_4} + \frac{{at_4^2}}{2}\]
Путь \(S_2\) за следующие 4 секунды найдем как разность путь за \(t_8=8\) секунд и пути за первые \(t_4=4\) секунды.
\[{S_2} = S\left( {{t_8}} \right) — S\left( {{t_4}} \right)\]
\[{S_2} = {\upsilon _0}{t_8} + \frac{{at_8^2}}{2} — \left( {{\upsilon _0}{t_4} + \frac{{at_4^2}}{2}} \right)\]
\[{S_2} = {\upsilon _0}\left( {{t_8} — {t_4}} \right) + \frac{{a\left( {t_8^2 — t_4^2} \right)}}{2}\]
В итоге получим такую систему уравнений с двумя неизвестными.
\[\left\{ \begin{gathered}
{S_1} = {\upsilon _0}{t_4} + \frac{{at_4^2}}{2} \hfill \\
{S_2} = {\upsilon _0}\left( {{t_8} — {t_4}} \right) + \frac{{a\left( {t_8^2 — t_4^2} \right)}}{2} \hfill \\
\end{gathered} \right.\]
Не будем даже пытаться решить эту задачу в общем виде, а сразу подставим в уравнения численные данные задачи. Всегда следите за тем, чтобы данные подставлялись только в единицах системы СИ.
\[\left\{ \begin{gathered}
24 = 4{\upsilon _0} + 8a \hfill \\
64 = 4{\upsilon _0} + 24a \hfill \\
\end{gathered} \right.\]
Нам нужно найти только начальную скорость \(\upsilon_0\), поэтому домножим первое уравнение на 3, и вычтем из первого уравнения второе.
\[\left\{ \begin{gathered}
72 = 12{\upsilon _0} + 24a \hfill \\
64 = 4{\upsilon _0} + 24a \hfill \\
\end{gathered} \right.\]
\[8{\upsilon _0} = 8\]
\[{\upsilon _0} = 1\; м/с = 3,6\; км/ч\]
Ответ: 3,6 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.39 Тело, имея некоторую начальную скорость, движется равноускоренно. За время
1.3.41 Частица, начав двигаться из состояния покоя и пройдя некоторый путь
1.3.42 Велосипедист начал свое движение из состояния покоя и в течение первых
Зачем такая сложность?
Если помнить, что
X(t) = X(0) + V(0) * t + a t^2 / 2
получим
X1 = V0*t1 + a*t1^2 /2
и для 2-ой точки
X2=S1+S2=V0*t2 + a*t2^2 / 2
или
24 = 4*V0 + 8 a
88 = 8*V0 + 32a
и ответ
V0 = 1 м/с
А путь за следующие 4сек равен 64 м. Но эта величина сумма 8 сек или отдельно новых 4 сек?
А то условие не понятное какое-то
За первые четыре секунды (т.е. за 1-ую, 2-ую, 3-ю, 4-ую секунды) тело проходит 24 м, за следующие четыре секунды (т.е. за 5-ую, 6-ую, 7-ую, 8-ую секунды) — 64 м.
Раз 64 м — это за новые секунды, то зачем вычитать старые?
Да, Вы можете использовать формулу:\[{S_2} = {\upsilon _{02}}t + \frac{{a{t^2}}}{2}\]Но вот \(\upsilon_{02}\) — это скорость точки в начале 5-ой секунды, которую Вы можете выразить только через искомую начальную скорость \(\upsilon_{0}\). Поэтому, чтобы не увеличивать количество неизвестных, используется логичное правило, что путь на n-ую секунду равен разности пути за n и (n-1) секунд.
Респектабельно, но так расписывать я не могу))
СПАСИБО!!!!!!!!!!!!!!!!!!