icodepro.ruУсловие задачи:
Три бруска, массы которых 0,5, 0,3 и 0,1 кг, связаны нитями и лежат на столе. К первому бруску приложена горизонтально направленная сила, равная 18 Н. Какова сила натяжения нити, связывающей первый и второй бруски? Трение не учитывать.
Задача №2.1.49 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=0,5\) кг, \(m_2=0,3\) кг, \(m_3=0,1\) кг, \(F=18\) Н, \(T_{12}-?\)
Решение задачи:
Важно понимать следующее: если бруски связаны нерастяжимой нитью, то у всех трех брусков будет одинаковое ускорение.
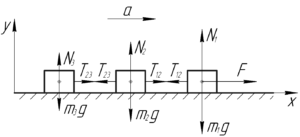
Помимо сил тяжести и сил реакции опоры на первый брусок действует сила \(F\) и сила натяжения \(T_{12}\), на второй — силы натяжения \(T_{12}\) и \(T_{23}\), на третий — только сила натяжения \(T_{23}\). Все это замечательно демонстрируется на схеме к рисунку.
Так как нас не интересуют силы, действующие вдоль оси \(y\), то запишем второй закон Ньютона для всех брусков в проекции на ось \(x\):
\[\left\{ \begin{gathered}
F — {T_{12}} = {m_1}a \;\;\;\;(1)\hfill \\
{T_{12}} — {T_{23}} = {m_2}a \;\;\;\;(2)\hfill \\
{T_{23}} = {m_3}a \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Из выражения (1) видно, что для нахождения искомой силы натяжения \(T_{12}\) следует знать ускорение \(a\). Чтобы найти ускорение \(a\), сложим все выражения системы, тогда мы избавимся от неизвестных сил натяжения.
\[F = \left( {{m_1} + {m_2} + {m_3}} \right)a\]
Это выражение также можно было получить, используя теорему о движении центра масс, если Вы её знаете, конечно. Ускорение равно:
\[a = \frac{F}{{{m_1} + {m_2} + {m_3}}}\]
Из выражения (1) выразим искомую силу натяжения \(T_{12}\).
\[{T_{12}} = F — {m_1}a\]
Подставим в это выражение полученную формулу для ускорения.
\[{T_{12}} = F — \frac{{F{m_1}}}{{{m_1} + {m_2} + {m_3}}} = \frac{{F\left( {{m_2} + {m_3}} \right)}}{{{m_1} + {m_2} + {m_3}}}\]
Посчитаем ответ:
\[{T_{12}} = \frac{{18\left( {0,3 + 0,1} \right)}}{{0,5 + 0,3 + 0,1}} = 8\; Н\]
Ответ: 8 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.48 Тело, брошенное вертикально вверх с начальной скоростью 30 м/с, достигло высшей
2.1.50 Тело массой 1,5 кг движется вверх по вертикальной стенке под действием силы 20 Н
2.1.51 Тело массой 100 кг движется по горизонтальной поверхности под действием силы
Как будет с силами трения?
а если у меня масса брусков 9,6,3 и сила равна 126H то какой ответ будет?
А почему мы не учитываем вес тела?
А зачем Вам вес? Вес — это сила, с которой тело действует на опору или подвес.
Может быть Вы имеете в виду массу тела? Массу тела (строго говоря, массу всех тел (брусков)) мы учитываем.
Или может быть Вы имеете в виду силу тяжести? Записывать проекции сил на ось \(y\), направленную перпендикулярно столу, нет смысла, так как в задаче есть указание не учитывать силу трения.
А если брусков 4 и надо найти силу натяжения между вторым и третим и трение учитывать?
Решаете точно также:\[\left\{ \begin{gathered}
F — {T_{12}} = {m_1}a \hfill \\
{T_{12}} — {T_{23}} = {m_2}a \hfill \\
{T_{23}} — {T_{34}} = {m_3}a \hfill \\
{T_{34}} = {m_4}a \hfill \\
\end{gathered} \right.\]Если все сложить, то получите:\[F = \left( {{m_1} + {m_2} + {m_3} + {m_4}} \right)a\]Откуда ускорение равно:\[a = \frac{F}{{{m_1} + {m_2} + {m_3} + {m_4}}}\]Если сложить первый два уравнения, то имеете:\[F — {T_{23}} = \left( {{m_1} + {m_2}} \right)a\]Тогда:\[{T_{23}} = F — \left( {{m_1} + {m_2}} \right)a\]Учитывая выражение для ускорения, получим:\[{T_{23}} = F — \frac{{F\left( {{m_1} + {m_2}} \right)}}{{{m_1} + {m_2} + {m_3} + {m_4}}}\]\[{T_{23}} = \frac{{F\left( {{m_3} + {m_4}} \right)}}{{{m_1} + {m_2} + {m_3} + {m_4}}}\]
А если брусков 6 и надо найти силу натяжения нити между 2 и 3, то как быть?
Запишите второй закон Ньютона для каждого бруска (будем думать, что у Вас в задаче написано, что трением пренебречь):\[\left\{ \begin{gathered}
F — {T_{12}} = {m_1}a \hfill \\
{T_{12}} — {T_{23}} = {m_2}a \hfill \\
{T_{23}} — {T_{34}} = {m_3}a \hfill \\
{T_{34}} — {T_{45}} = {m_4}a \hfill \\
{T_{45}} — {T_{56}} = {m_5}a \hfill \\
{T_{56}} = {m_6}a \hfill \\
\end{gathered} \right.\]
Если сложить все эти уравнения, то получим:\[F = \left( {{m_1} + {m_2} + {m_3} + {m_4} + {m_5} + {m_6}} \right)a\]Откуда ускорение, с которым движутся бруски, равно:\[a = \frac{F}{{{m_1} + {m_2} + {m_3} + {m_4} + {m_5} + {m_6}}}\]Вы могли получить это также из теоремы о движении центра масс, если, конечно, знаете её.
Чтобы найти \(T_{23}\) нужно сложить первые уравнения:\[F — {T_{23}} = \left( {{m_1} + {m_2}} \right)a\]\[{T_{23}} = F — \left( {{m_1} + {m_2}} \right)a\]Учитывая выражение для ускорения, имеем:\[{T_{23}} = F — \frac{{\left( {{m_1} + {m_2}} \right)F}}{{{m_1} + {m_2} + {m_3} + {m_4} + {m_5} + {m_6}}}\]\[{T_{23}} = F\frac{{{m_3} + {m_4} + {m_5} + {m_6}}}{{{m_1} + {m_2} + {m_3} + {m_4} + {m_5} + {m_6}}}\]
Я не уверена, но разве не нужно было учитывать силу трения о поверхность?
В условии написано: «Трение не учитывать»