Условие задачи:
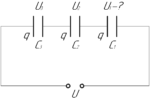
Три конденсатора электроемкостью 0,1, 0,125 и 0,5 мкФ соединены последовательно и подключены к источнику напряжения 800 В. Какая разность потенциалов будет на первом конденсаторе?
Задача №6.4.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(C_1=0,1\) мкФ, \(C_2=0,125\) мкФ, \(C_3=0,5\) мкФ, \(U=800\) В, \(U_1-?\)
Решение задачи:
 Все подобные задачи решаются одинаковым образом, сначала запишем формулу электроемкости и выразим из этой формулы заряд \(q\) (она нам понадобится для дальнейших объяснений):
Все подобные задачи решаются одинаковым образом, сначала запишем формулу электроемкости и выразим из этой формулы заряд \(q\) (она нам понадобится для дальнейших объяснений):
\[C = \frac{q}{U}\]
\[q = CU\;\;\;\;(1)\]
Пусть \(U_1\) — разность потенциалов между обкладками первого конденсатора, \(U_2\) — разность потенциалов между обкладками второго, а \(U_3\) — разность потенциалов между обкладками третьего. Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый, а общее напряжение равно сумме напряжений на каждом из конденсаторов. Учитывая все написанное и пользуясь формулой (1), мы можем получить такую систему:
\[\left\{ \begin{gathered}
{C_1}{U_1} = {C_2}{U_2} = {C_3}{U_3} \hfill \\
U = {U_1} + {U_2} + {U_3} \hfill \\
\end{gathered} \right.\]
Поскольку в задаче нам необходимо определить напряжение \(U_1\) на первом конденсаторе, то из верхнего равенства системы выразим напряжения \(U_2\) и \(U_3\) через искомое \(U_1\):
\[{U_2} = {U_1}\frac{{{C_1}}}{{{C_2}}}\;\;\;\;(2)\]
\[{U_3} = {U_1}\frac{{{C_1}}}{{{C_3}}}\;\;\;\;(3)\]
Полученные выражение (2) и (3) подставим в нижнее равенство системы:
\[U = {U_1} + {U_1}\frac{{{C_1}}}{{{C_2}}} + {U_1}\frac{{{C_1}}}{{{C_3}}}\]
Приведем правую часть под общий знаменатель:
\[U = {U_1}\frac{{{C_2}{C_3} + {C_1}{C_3} + {C_1}{C_2}}}{{{C_2}{C_3}}}\]
Откуда напряжение на первом конденсаторе \(U_1\) равно:
\[{U_1} = \frac{{U{C_2}{C_3}}}{{{C_1}{C_2} + {C_2}{C_3} + {C_1}{C_3}}}\]
Задача решена в общем виде, посчитаем численный ответ:
\[{U_1} = \frac{{800 \cdot 0,125 \cdot {{10}^{ — 6}} \cdot 0,5 \cdot {{10}^{ — 6}}}}{{0,1 \cdot {{10}^{ — 6}} \cdot 0,125 \cdot {{10}^{ — 6}} + 0,125 \cdot {{10}^{ — 6}} \cdot 0,5 \cdot {{10}^{ — 6}} + 0,1 \cdot {{10}^{ — 6}} \cdot 0,5 \cdot {{10}^{ — 6}}}} = 400\;В = 0,4\;кВ\]
Ответ: 0,4 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.31 Бумага пробивается при напряженности поля 18 кВ/см. Два плоских конденсатора с изолятором
6.4.33 Три воздушных конденсатора емкостью 1 мкФ каждый соединены последовательно
6.4.34 Батарея из 5 последовательно соединенных конденсаторов емкостью 4 мкФ каждый

 icodepro.ru
icodepro.ru
Какой электроёмкостью обладает миелиновая оболочка участка цилиндрического нервного волокна длины 5 мм, если его радиус 8 мкм и толщина миелинового слоя 1,5 мкм? Диэлектрическая проницаемость мембраны 45. Расчёт провести по формуле ёмкости плоского конденсатора.
Скорее расчет нужно провести по формуле цилиндрического конденсатора, а не плоского:\[C = \frac{{2\pi \varepsilon {\varepsilon _0}l}}{{\ln \frac{{{r_2}}}{{{r_1}}}}}\]Применительно к нашей задаче:\[C = \frac{{2\pi \varepsilon {\varepsilon _0}l}}{{\ln \frac{{{r_1} + \delta }}{{{r_1}}}}}\]\[C = \frac{{2 \cdot 3,14 \cdot 45 \cdot 8,85 \cdot {{10}^{ — 12}} \cdot 5 \cdot {{10}^{ — 3}}}}{{\ln \frac{{8 \cdot {{10}^{ — 6}} + 1,5 \cdot {{10}^{ — 6}}}}{{8 \cdot {{10}^{ — 6}}}}}} = 7,28 \cdot {10^{ — 11}}\;Ф = 72,8\;пФ\]
Спасибо)))