Условие задачи:
В двух противоположных вершинах квадрата со стороной 30 см находятся заряды по 0,2 мкКл. Найти напряженность поля в двух других вершинах квадрата.
Задача №6.2.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a=30\) см, \(q=0,2\) мкКл, \(E-?\)
Решение задачи:
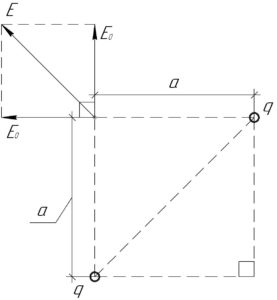 Так как квадрат симметричен относительно диагонали, и в противоположных вершинах квадрата расположены одинаковые заряды, то в двух других вершинах квадрата напряженности поля будут одинаковыми (по модулю). Поэтому достаточно найти напряженность поля \(E\) только в одной вершине.
Так как квадрат симметричен относительно диагонали, и в противоположных вершинах квадрата расположены одинаковые заряды, то в двух других вершинах квадрата напряженности поля будут одинаковыми (по модулю). Поэтому достаточно найти напряженность поля \(E\) только в одной вершине.
Каждый из зарядов \(q\) будет создавать в этой вершине электростатическое поле напряженностью \(E_0\), равное:
\[{E_0} = \frac{{kq}}{{{a^2}}}\;\;\;\;(1)\]
Коэффициент пропорциональности \(k\) равен 9·109 Н·м2/Кл2.
Вектор напряженности результирующего электрического поля \(\overrightarrow E\) равен векторной сумме напряженностей полей \(\overrightarrow {{E_0}}\) от каждого из зарядов. Так как между векторами \(\overrightarrow {{E_0}}\) угол равен 90° (как и между сторонами в квадрате), то по теореме Пифагора имеем:
\[E = \sqrt {E_0^2 + E_0^2} \]
\[E = {E_0}\sqrt 2 \]
Принимая во внимание равенство (1), получим:
\[E = \frac{{\sqrt 2 kq}}{{{a^2}}}\]
Численное значение напряженности поля \(E\) равно:
\[E = \frac{{\sqrt 2 \cdot 9 \cdot {{10}^9} \cdot 0,2 \cdot {{10}^{ — 6}}}}{{{{0,3}^2}}} = 28284,3\;В/м \approx 28,3\;кВ/м\]
Ответ: 28,3 кВ/м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.25 В серединах всех сторон равностороннего треугольника расположены одинаковые
6.2.27 В трёх вершинах квадрата со стороной 30 см находятся точечные заряды
6.2.28 В трёх вершинах квадрата со стороной 1 м находятся положительные точечные заряды

 icodepro.ru
icodepro.ru
И наверное не а^2, a r^2
Все поправил!
Спасибо, что сообщили о неточностях!
В дано написано 3м, может 0,3 м?