Условие задачи:
В колено U-образной трубки площадью 1 см2, содержащей ртуть, налили 7,2 г воды и 20 г бензина. На сколько уровень жидкости в одном колене станет выше, чем в другом?
Задача №3.1.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=1\) см2, \(m_{в}=7,2\) г, \(m_{б}=20\) г, \(\Delta h-?\)
Решение задачи:
\[\Delta h = {h_б} + {h_в} — {h_{рт}}\;\;\;\;(1)\]
Первые два слагаемых найдем по следующим формулам (по сути — формула нахождения объема через массу и плотность):
\[\left\{ \begin{gathered}
{h_б} = \frac{{{m_б}}}{{{\rho _б}S}} \hfill \\
{h_в} = \frac{{{m_в}}}{{{\rho _в}S}} \hfill \\
\end{gathered} \right.\]
Выделим на схеме горизонтальный уровень, ниже которого находится только ртуть. Закон сообщающихся сосудов говорит о том, что при равновесии давление жидкости на одном горизонтальном уровне одинаково, поэтому справедливо записать:
\[{p_{рт}} = {p_{б}} + {p_{в}}\;\;\;\;(2)\]
Давление столбика ртути высотой \(h_{рт}\) равно:
\[{p_{рт}} = {\rho _{рт}}g{h_{рт}}\]
Давление бензина и воды найдем по формуле-определению давления:
\[\left\{ \begin{gathered}
{p_б} = \frac{{{m_б}g}}{S} \hfill \\
{p_в} = \frac{{{m_в}g}}{S} \hfill \\
\end{gathered} \right.\]
Равенство (2) примет следующий вид:
\[{\rho _{рт}}g{h_{рт}} = \frac{{{m_б}g}}{S} + \frac{{{m_в}g}}{S}\]
\[{h_{рт}} = \frac{{{m_б}}}{{{\rho _{рт}}S}} + \frac{{{m_в}}}{{{\rho _{рт}}S}}\]
В конечном счете формула (1) станет такой:
\[\Delta h = \frac{{{m_б}}}{{{\rho _б}S}} + \frac{{{m_в}}}{{{\rho _в}S}} — \frac{{{m_б}}}{{{\rho _{рт}}S}} — \frac{{{m_в}}}{{{\rho _{рт}}S}}\]
\[\Delta h = \frac{1}{S}\left( {\frac{{{m_б}}}{{{\rho _б}}} + \frac{{{m_в}}}{{{\rho _в}}} — \frac{{{m_б}}}{{{\rho _{рт}}}} — \frac{{{m_в}}}{{{\rho _{рт}}}}} \right)\]
Переведем некоторые величины в систему СИ:
\[1\;см^2 = {10^{ — 4}}\;м^2\]
\[7,2\;г = 0,0072\;кг\]
\[20\;г = 0,02\;кг\]
Плотность бензина \(\rho_{б}\) равна 700 кг/м3, плотность воды \(\rho_{в}\) — 1000 кг/м3, плотность ртути \(\rho_{рт}\) равна 13600 кг/м3. Произведем вычисление ответа:
\[\Delta h = \frac{1}{{{{10}^{ — 4}}}}\left( {\frac{{0,02}}{{700}} + \frac{{0,0072}}{{1000}} — \frac{{0,02}}{{13600}} — \frac{{0,0072}}{{13600}}} \right) = 0,338\;м = 338\;мм\]
Ответ: 338 мм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.37 В сосуд с водой вставлена трубка сечением 2 см2. В трубку налили 72 г масла. Найти
3.1.39 В сообщающиеся сосуды налили сначала ртуть. Затем в один сосуд налили масло высотой
3.1.40 В сообщающихся сосудах находится ртуть. Площадь сечения одного сосуда в 4 раза

 icodepro.ru
icodepro.ru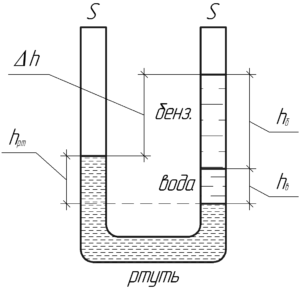
вы неправильно указали ответ в миллиметрах