icodepro.ruУсловие задачи:
В покоящийся шар массой 1 кг, подвешенный на стержне, попадает пуля массой 0,01 кг, летящая под углом 45° к стержню, и застревает в нем. После удара пуля с шаром откачнулись на высоту 0,02 м. Найти скорость пули.
Задача №2.10.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=1\) кг, \(m=0,01\) кг, \(\alpha=45^\circ\), \(h=0,02\) м, \(\upsilon-?\)
Решение задачи:
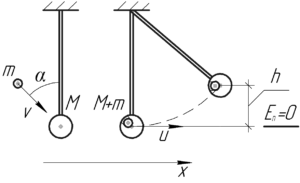Так как пуля застревает в шаре, то в данном случае мы имеем дело с абсолютно неупругим ударом. Вдоль горизонтальной оси на шар и пулю не действуют никакие силы, то есть система из этих тел замкнута вдоль этой оси. Запишем закон сохранения импульса до и после удара в проекции на эту ось:
\[m\upsilon \cdot \sin \alpha = \left( {m + M} \right)u\]
Выразим скорость пули \(u\) до удара:
\[\upsilon = \frac{{\left( {m + M} \right)u}}{{m\sin \alpha }}\;\;\;\;(1)\]
После удара шар начнет двигаться и вскоре достигнет максимальной высоты \(h\). По закону сохранения энергии:
\[\frac{{\left( {M + m} \right){u^2}}}{2} = \left( {M + m} \right)gh\]
Откуда скорость шара \(u\) с застрявшей в нём после удара пулей равна:
\[u = \sqrt {2gh} \;\;\;\;(2)\]
Подставим (2) в (1), так мы получим решение этой задачи в общем виде.
\[\upsilon = \frac{{\left( {m + M} \right)\sqrt {2gh} }}{{m\sin \alpha }}\]
Все данные задачи известны и даны в системе СИ, можем приступать к расчету ответа:
\[\upsilon = \frac{{\left( {0,01 + 1} \right)\sqrt {2 \cdot 10 \cdot 0,02} }}{{0,01 \cdot \sin 45^\circ }} = 90,34\; м/с = 325,21\; км/ч\]
Ответ: 325,21 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.24 Мальчик, стоя на Земле, бросает камень горизонтально со скоростью 5 м/с
2.10.26 Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового
2.10.27 Два груза массами 0,04 и 0,01 кг соединены невесомой нитью, переброшенной
Как найти h?
Запишем закон сохранения импульса до и после удара в проекции на ось \(x\):\[m\upsilon \cdot \sin \alpha = \left( {m + M} \right)u\]Откуда скорость \(u\) равна:\[u = \frac{{m\upsilon \sin \alpha }}{{M + m}}\]По закону сохранения энергии:\[\frac{{\left( {M + m} \right){u^2}}}{2} = \left( {M + m} \right)gh\]Откуда высота \(h\):\[h = \frac{{{u^2}}}{{2g}}\]В итоге имеем:\[h = \frac{{{m^2}{\upsilon ^2}{{\sin }^2}\alpha }}{{2g{{\left( {M + m} \right)}^2}}}\]
Пуля, летящая горизонтально со скоростью v — 610 м\с, попадает в шар,
подвешенный на невесомом жёстком стержне, и застревает в нем. Масса пули –
m — 3,9 г, масса шара – М ?. Расстояние от центра шара до точки подвеса стержня l -?. От
удара пули стержень с шаром отклонился на угол ? — 22 градуса, поднявшись на высоту h — 3,3, найти недостающие величины. Принять
g=10 м/с2.
Для нахождения массы шара достаточно записать законы сохранения импульса и энергии:\[\left\{ \begin{gathered}
m\upsilon = \left( {m + M} \right)u\;\;\;\;(1) \hfill \\
\frac{{\left( {m + M} \right){u^2}}}{2} = \left( {m + M} \right)gh\;\;\;\;(2) \hfill \\
\end{gathered} \right.\]Из (2) находим скорость шара после попадания в него пули:\[u = \sqrt {2gh} \]Из (1) выразим массу шара, для чего раскроем скобки в правой части:\[m\upsilon = mu + Mu\]\[m\upsilon — mu = Mu\]\[m\left( {\upsilon — u} \right) = Mu\]\[M = \frac{{m\left( {\upsilon — u} \right)}}{u}\]Учитывая выражения для нахождения скорости \(u\), имеем:\[M = \frac{{m\left( {\upsilon — \sqrt {2gh} } \right)}}{{\sqrt {2gh} }}\]Избавлюсь от иррациональности в знаменателе:\[M = \frac{{m\left( {\upsilon \sqrt {2gh} — 2gh} \right)}}{{2gh}}\]Численное значение массы шара равно:\[M = \frac{{0,0039 \cdot \left( {610 \cdot \sqrt {2 \cdot 10 \cdot 3,3} — 2 \cdot 10 \cdot 3,3} \right)}}{{2 \cdot 10 \cdot 3,3}} = 0,289\;кг\]Длину стержня можно найти из геометрических соображений:\[h = l — l\cos \alpha \]\[h = l\left( {1 — \cos \alpha } \right)\]\[l = \frac{h}{{1 — \cos \alpha }}\]\[l = \frac{{3,3}}{{1 — \cos 22^\circ }} = 45,3\;м\]Почему-то длина получилась огромной, но Вы не привели единицы измерения высоты, поэтому я считал, что она дана в метрах.
спасибочки, огромное! в метрах всё правильно!
в см, а не в метрах, жаль что допустила ошибку! как быть если в см?
\[M = \frac{{0,0039 \cdot \left( {610 \cdot \sqrt {2 \cdot 10 \cdot 0,033} – 2 \cdot 10 \cdot 0,033} \right)}}{{2 \cdot 10 \cdot 0,033}} = 2,93\;кг\]\[l = \frac{{0,033}}{{1 – \cos 22^\circ }} = 0,453\;м\]
m?·sin?=(m+M)u
Вообще-то косинус альфа…
Смотрите рисунок внимательно, нужен противолежащий к углу ? катет — значит синус.