Решение: В серединах всех сторон равностороннего треугольника расположены одинаковые

Условие задачи:

В серединах всех сторон равностороннего треугольника расположены одинаковые точечные заряды 1 нКл. В двух вершинах этого треугольника помещены точечные заряды -4 нКл каждый. Длина стороны треугольника 2 м. Определить напряженность электрического поля в третьей вершине треугольника.

Задача №6.2.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q_1=1\) нКл, \(q_2=-4\) нКл, \(l=\frac{r}{2}\), \(r=2\) м, \(E-?\)

Решение задачи:

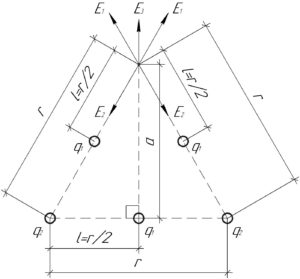Для начала найдём суммарный вектор напряженности электрического поля \(E_0\), создаваемого зарядами \(q_1\) и \(q_2\), лежащими на одной стороне треугольника, в третьей вершине равностороннего треугольника. Каждый из этих зарядов будет создавать электрическое поле напряженностью \(E_1\) и \(E_2\) соответственно, модуль которых можно определить по формулам:

\[\left\{ \begin{gathered}
{E_1} = \frac{{k{q_1}}}{{{l^2}}} \hfill \\
{E_2} = \frac{{k\left| {{q_2}} \right|}}{{{r^2}}} \hfill \\
\end{gathered} \right.\]

Коэффициент пропорциональности \(k\) равна 9·10⁹ Н·м²/Кл².

По условию заряды \(q_1\) расположены в серединах сторон треугольника, то есть \(l=\frac{r}{2}\). Учитывая это и раскрывая модуль во второй формуле (так как \({q_2} < 0\), то \(\left| {{q_2}} \right| = — {q_2}\)), то получим:

\[\left\{ \begin{gathered}
{E_1} = \frac{{4k{q_1}}}{{{r^2}}} \hfill \\
{E_2} = \frac{{ — k{q_2}}}{{{r^2}}} \hfill \\
\end{gathered} \right.\]

Поскольку вектора \(\overrightarrow {{E_1}}\) и \(\overrightarrow {{E_2}}\) противонаправлены (так как заряды \(q_1\) и \(q_2\) имеют разные знаки), то модуль суммарного вектора напряженности электрического поля \(E_0\), создаваемого зарядами \(q_1\) и \(q_2\) в третьей вершине равностороннего треугольника, равен:

\[{E_0} = {E_1} — {E_2}\]

\[{E_0} = \frac{{4k{q_1}}}{{{r^2}}} — \left( {\frac{{ — k{q_2}}}{{{r^2}}}} \right)\]

\[{E_0} = \frac{k}{{{r^2}}}\left( {4{q_1} + {q_2}} \right)\]

Любопытства ради посчитаем численное значение:

\[{E_0} = \frac{{9 \cdot {{10}^9}}}{{{2^2}}}\left( {4 \cdot 1 \cdot {{10}^{ — 9}} + \left( { — 4 \cdot {{10}^{ — 9}}} \right)} \right) = 0\;В/м\]

Значит суммарное электрическое поле в третьей вершине треугольника, создаваемое четырьмя зарядами \(q_1\) и \(q_2\), лежащими на боковых сторонах треугольника, равно нулю. Поэтому искомая напряженность поля \(E\) равна напряженности поля \(E_3\), создаваемого зарядом \(q_1\), лежащим в середине основания треугольника (смотрите схему).

\[E = {E_3}\]

\[{E_3} = \frac{{k{q_1}}}{{{a^2}}}\]

Здесь \(a\) — длина высоты равностороннего треугольника. Высота в равностороннем треугольнике является ещё и медианой (так как равносторонний треугольник — частный случай равнобедренного). Поэтому из теоремы Пифагора имеем:

\[{a^2} = {r^2} — \frac{{{r^2}}}{4}\]

\[{a^2} = \frac{{3{r^2}}}{4}\]

Тогда:

\[{E_3} = \frac{{4k{q_1}}}{{3{r^2}}}\]

В итоге имеем:

\[E = \frac{{4k{q_1}}}{{3{r^2}}}\]

Произведем вычисления:

\[E = \frac{{4 \cdot 9 \cdot {{10}^9} \cdot 1 \cdot {{10}^{ — 9}}}}{{3 \cdot {2^2}}} = 3\;В/м = 0,03\;В/см\]