icodepro.ruУсловие задачи:
В сосуд, имеющий форму прямоугольной призмы, шириной 15 см и длиной 35 см налита жидкость. Какова высота уровня жидкости в сосуде, если сила её давления на дно равна силе давления на боковую поверхность сосуда?
Задача №3.2.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a=15\) см, \(b=35\) см, \(P_{дн}=P_{б}\), \(h-?\)
Решение задачи:
В общем случае сила давления равна произведению давления на площадь:
\[P = pS\]
Поэтому:
\[\left\{ \begin{gathered}
{P_{дн}} = {p_{дн}}{S_{дн}} \hfill \\
{P_б} = {p_б}{S_б} \hfill \\
\end{gathered} \right.\]
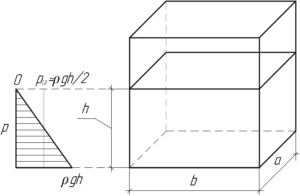
Давление жидкости возрастает пропорционально глубине: на уровне поверхности жидкости оно равно нулю, на глубине \(h\) — величине \(\rho gh\). Воздействие воды на боковую стенку сосуда характеризуют средним давлением, равным \(\rho g \frac{h}{2}\). Таким образом:
\[\left\{ \begin{gathered}
{p_{дн}} = \rho gh \hfill \\
{p_б} = \rho g\frac{h}{2} \hfill \\
\end{gathered} \right.\]
Площадь дна сосуда и его боковой поверхности можно найти по следующим формулам (если непонятно, то смотрите схему):
\[\left\{ \begin{gathered}
{S_{дн}} = ab \hfill \\
{S_б} = 2\left( {ah + bh} \right) \hfill \\
\end{gathered} \right.\]
В итоге:
\[\left\{ \begin{gathered}
{P_{дн}} = \rho gh \cdot ab \hfill \\
{P_б} = \rho g\frac{h}{2} \cdot 2\left( {ah + bh} \right) \hfill \\
\end{gathered} \right.\]
По условию \(P_{дн}=P_{б}\), а это значит, что:
\[\rho gh \cdot ab = \rho gh \cdot \left( {ah + bh} \right)\]
\[ab = h\left( {a + b} \right)\]
\[h = \frac{{ab}}{{a + b}}\]
Высота уровня жидкости равна:
\[h = \frac{{15 \cdot 35}}{{15 + 35}} = 10,5\;см = 0,1 м\]
Ответ: 0,1 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.2.5 Аквариум наполнен доверху водой. С какой средней силой давит вода на стенку
3.2.7 На сколько отличается давление столбика ртути высотой 10 мм от давления столбика
3.2.8 Найти давление в озере на глубине 4,5 м. Атмосферное давление
P=pS
что это за формула? разве она существует? в интернете про неё ноль информации
вы объяснили как:
сила давления равна произведению давления на площадь
а чем тогда сила давления отличается от давления которое p ??
давление же и есть сила…
получается что P=pS всё равно что x = x*y как-то страннно…
Посмотрите на поясняющий рисунок. Давление это линейная функция высоты. Среднее давление находим как разницу между конечным и начальным давлением деленную пополам.
Я Вас поправлю, как сумму, а не как разность
«Давление не зависит от объема и формы сосуда. Оно зависит только от плотности и высоты столба конкретной жидкости в данном случае. Из чего следует, что, давления газа на дно и стенки сосуда будет одинаковым»-Вы согласны с этим утверждением? Если да, то оно разве не противоречит утверждению:»Воздействие воды на боковую стенку сосуда характеризуют средним давлением, равным ?gh/2″?
Скажу, что это утверждение нелогичное. «Давление не зависит от объема и формы сосуда. Оно зависит только от плотности и высоты столба конкретной жидкости в данном случае. Из чего следует, что, давление газа на дно и стенки сосуда будет одинаковым». Что из чего следует, я не понял. И с каких это пор жидкость одно и то же, что и газ.
Если же оставить только первые два предложения, то противоречия не вижу.
Вместо слово газ ,должно стоять слово жидкость, я перепутал случайно. Давление в любой точки сосуда на одинаковой высоте одинаково, верно ? Если да то, что это за формула ?gh/2 ?
Это среднее давление на стенку. Боковая стенка — это же протяженный объект, а не точка, поэтому в каждой точке боковой стенки по вертикали давление жидкости разное. Для того, чтобы найти силу давления на стенку, нам необходимо найти среднее давление, то есть давление, с которым жидкость в среднем давит на боковую стенку.
Разве давление жидкости на точку стенки не будет равно давлению на высоте этой точки ? То есть, давление на стенку ?gh=p.
Давление на стенку в точке и среднее давление на всю стенку — это разные вещи. Первая вычисляется по формуле p=?gh, вторая — по формуле p_ср=?gh/2.
Среднее давление на стенку необходимо для вычисления силы давления жидкости на стенку.