Условие задачи:
В трубке длиной 1,73 м, заполненной газом, находится столбик ртути длиной 30 мм. Когда трубка расположена вертикально, ртуть делит трубку на две равные части. Давление газа над ртутью 8 кПа. На какое расстояние сдвинется ртуть, если трубку положить горизонтально?
Задача №4.3.39 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(L=1,73\) м, \(h=30\) мм, \(p_1=8\) кПа, \(\Delta l -?\)
Решение задачи:
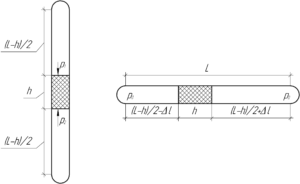 Рисунок к задаче представлен справа. Температура тех двух частей газа, которые есть в трубке, в процессе переворачивания трубки не изменится (\(T=const\)), поэтому мы можем записать 2 раза закон Бойля-Мариотта. Также, для того момента, когда трубка еще расположена вертикально, запишем закон Паскаля. В итоге:
Рисунок к задаче представлен справа. Температура тех двух частей газа, которые есть в трубке, в процессе переворачивания трубки не изменится (\(T=const\)), поэтому мы можем записать 2 раза закон Бойля-Мариотта. Также, для того момента, когда трубка еще расположена вертикально, запишем закон Паскаля. В итоге:
\[\left\{ \begin{gathered}
{p_1}S\frac{{L — h}}{2} = {p_0}S\left( {\frac{{L — h}}{2} — \Delta l} \right)\,\,\,\,(1) \hfill \\
{p_2}S\frac{{L — h}}{2} = {p_0}S\left( {\frac{{L — h}}{2} + \Delta l} \right)\,\,\,\,(2) \hfill \\
{p_1} + \rho gh = {p_2}\,\,\,\,(3) \hfill \\
\end{gathered} \right.\]
Поделим выражение (2) на выражение (1), тогда:
\[\frac{{{p_2}}}{{{p_1}}} = \frac{{L — h + 2\Delta l}}{{L — h — 2\Delta l}}\]
Теперь воспользуемся выражением (3), а также представим в числителе правой части \(2\Delta l = — 2\Delta l + 4\Delta l\).
\[\frac{{{p_1} + \rho gh}}{{{p_1}}} = \frac{{L — h — 2\Delta l + 4\Delta l}}{{L — h — 2\Delta l}}\]
\[1 + \frac{{\rho gh}}{{{p_1}}} = 1 + \frac{{4\Delta l}}{{L — h — 2\Delta l}}\]
\[\frac{{\rho gh}}{{{p_1}}} = \frac{{4\Delta l}}{{L — h — 2\Delta l}}\]
Из-за того, что искомое \(\Delta l\) присутствует и в числителе и в знаменателе правой части, перемножим дробь «крест-накрест»:
\[\rho ghL — \rho g{h^2} — 2\rho gh\Delta l = 4{p_1}\Delta l\]
Слагаемые с \(\Delta l\) перенесем в одну сторону, вынесем \(\Delta l\) за скобки и получим формулу для вычисления ответа в общем виде:
\[2\Delta l\left( {2{p_1} + \rho gh} \right) = \rho gh\left( {L — h} \right)\]
\[\Delta l = \frac{{\rho gh\left( {L — h} \right)}}{{2\left( {2{p_1} + \rho gh} \right)}}\]
Подставим численно исходные данные в системе СИ и вычислим ответ:
\[\Delta l = \frac{{13600 \cdot 10 \cdot 0,03 \cdot \left( {1,73 — 0,03} \right)}}{{2\left( {2 \cdot 8 \cdot {{10}^3} + 13600 \cdot 10 \cdot 0,03} \right)}} = 0,173\; м\]
Ответ: 0,173 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.3.38 Открытую с обеих сторон стеклянную трубку длиной 60 см
4.3.40 В каком из изображенных на рисунке процессов, проведенных
4.3.41 Горизонтально расположенный закрытый цилиндрический сосуд

 icodepro.ru
icodepro.ru