Условие задачи:
В цилиндрическое ведро с площадью дна 0,02 м2 налита вода. Найдите массу воды, если давление на боковую стенку ведра на расстоянии 0,1 м от дна равно 1960 Па.
Задача №3.2.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=0,02\) м2, \(h=0,1\) м, \(p=1960\) Па, \(m-?\)
Решение задачи:
 Массу воды \(m\) в цилиндрическом ведре легко найти по следующей формуле:
Массу воды \(m\) в цилиндрическом ведре легко найти по следующей формуле:
\[m = \rho V = \rho SH\;\;\;\;(1)\]
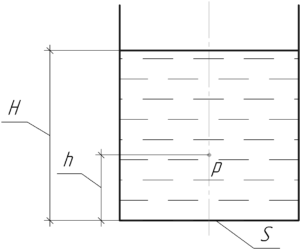
Давление воды на расстоянии \(h\) от дна найдем по формуле давления столба жидкости (смотрите схему):
\[p = \rho g\left( {H — h} \right)\]
Выразим высоту воды в ведре \(H\):
\[H = \frac{p}{{\rho g}} + h\]
Полученное подставим в формулу (1):
\[m = \rho S\left( {\frac{p}{{\rho g}} + h} \right)\]
Задача решена в общем виде. Учитывая, что плотность воды \(\rho\) равна 1000 кг/м3, то можно посчитать ответ:
\[m = 1000 \cdot 0,02 \cdot \left( {\frac{{1960}}{{1000 \cdot 10}} + 0,1} \right) = 5,92\; кг\]
Ответ: 5,92 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.2.13 В цилиндрический сосуд налиты равные по массе количества воды и ртути. Общая
3.2.15 Какова сила давления на поршень насоса при высоте подачи воды 25 м, если
3.2.16 На какой глубине в пресной воде давление в 3 раза больше нормального

 icodepro.ru
icodepro.ru