Условие задачи:
В углах квадрата со стороной 4 см поместили 4 электрона. Под действием электрических сил электроны разлетаются. Определить их скорости на бесконечности.
Задача №6.3.50 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a=4\) см, \(\upsilon-?\)
Решение задачи:
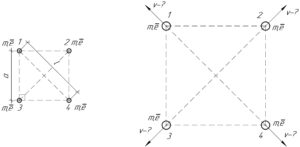 Перед нами хороша задача на применение закона сохранения энергии. Понятно, что начальная потенциальная энергия взаимодействия электронов \(W_п\) на бесконечности полностью перейдёт в их кинетическую энергию \(W_к\).
Перед нами хороша задача на применение закона сохранения энергии. Понятно, что начальная потенциальная энергия взаимодействия электронов \(W_п\) на бесконечности полностью перейдёт в их кинетическую энергию \(W_к\).
\[{W_п} = {W_к}\;\;\;\;(1)\]
Чтобы найти полную потенциальную энергию взаимодействия электронов, необходимо сложить все попарные потенциальные энергии взаимодействия электронов. Если обозначить электроны цифрами 1, 2, 3, 4 (как мы это сделали на схеме), то таких пар будет шесть: 1-2, 1-3, 1-4, 2-3, 2-4, 3-4. Заметьте, что расстояние между электронами в четырёх парах (1-2, 1-3, 2-4, 3-4) равно длине стороны квадрата \(a\), а в двух парах (1-4 и 2-3) — некоторой величине \(l\), значение которой найдём по теореме Пифагора:
\[{l^2} = {a^2} + {a^2}\]
\[{l^2} = 2{a^2}\]
\[l = a\sqrt 2\;\;\;\;(2)\]
Тогда потенциальная энергия \(W_п\) равна:
\[{W_п} = \frac{{4k{e^2}}}{a} + \frac{{2k{e^2}}}{l}\]
Здесь \(k\) — коэффициент пропорциональности, равный 9·109 Н·м2/Кл2, \(e\) — элементарный заряд, равный 1,6·10-19 Кл.
Принимая во внимание равенство (2), имеем:
\[{W_п} = \frac{{4k{e^2}}}{a} + \frac{{2k{e^2}}}{{a\sqrt 2 }}\]
\[{W_п} = \frac{{4k{e^2}}}{a} + \frac{{\sqrt 2 k{e^2}}}{a}\]
\[{W_п} = \frac{{\left( {4 + \sqrt 2 } \right)k{e^2}}}{a}\;\;\;\;(3)\]
На бесконечности скорости всех электронов будет одинаковыми (из-за закона сохранения импульса) и равны \(\upsilon\). Полная кинетическая энергия электронов \(W_к\) при этом будет равна:
\[{W_к} = 4\frac{{m{\upsilon ^2}}}{2}\]
\[{W_к} = 2m{\upsilon ^2}\;\;\;\;(4)\]
В полученной формуле \(m\) — масса электрона, равная 9,1·10-31 кг. С учётом (3) и (4) равенство (1) примет такой вид:
\[\frac{{\left( {4 + \sqrt 2 } \right)k{e^2}}}{a} = 2m{\upsilon ^2}\]
Откуда искомая скорость электронов \(\upsilon\) равна:
\[\upsilon = e\sqrt {\frac{{\left( {4 + \sqrt 2 } \right)k}}{{2ma}}} \]
Посчитаем численный ответ:
\[\upsilon = 1,6 \cdot {10^{ — 19}} \cdot \sqrt {\frac{{\left( {4 + \sqrt 2 } \right) \cdot 9 \cdot {{10}^9}}}{{2 \cdot 9,1 \cdot {{10}^{ — 31}} \cdot 0,04}}} = 130,9\;м/с\]
Ответ: 130,9 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.49 Найти скорость, которую приобретает электрон, пролетевший в электрическом поле
6.3.51 Электрон, ускоренный разностью потенциалов 5 кВ, влетает в середину зазора между
6.3.52 Маленький металлический шарик массой 1 г и зарядом 100 нКл брошен издалека

 icodepro.ru
icodepro.ru