Условие задачи:

В воде плавает льдина с площадью поперечного сечения 5 м² и высотой 0,5 м. Какую работу надо совершить, чтобы полностью погрузить льдину в воду?

Задача №3.3.46 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S=5\) м², \(h=0,5\) м, \(A-?\)

Решение задачи:

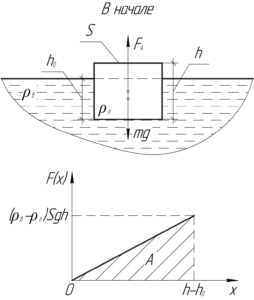Изначально льдина плавает, запишем условие плавания льдины:

\[{F_А} = mg\]

Распишем силу Архимеда в левой части и массу — в правой, получим:

\[{\rho _в}gS{h_0} = {\rho _л}Shg\;\;\;\;(1)\]

\[{h_0} = \frac{{{\rho _л}}}{{{\rho _в}}}h\;\;\;\;(2)\]

Отлично, теперь мы знаем \(h_0\) — высоту, на которую погружена льдина в начале.

Чтобы погрузить льдину в воду, нужно приложить к ней некоторую внешнюю силу \(F\). Если погружать льдину медленно, то есть с почти нулевой скоростью и ускорением, то значение силы \(F\) можно узнать из первого закона Ньютона.

Так как с увеличением глубины погружения льдины сила Архимеда будет возрастать, значит сила \(F\) будет переменной. Обозначим перемещение буквой \(x\), тогда:

\[F\left( x \right) = {F_А}\left( x \right) — mg\]

\[F\left( x \right) = {\rho _в}gS\left( {{h_0} + x} \right) — {\rho _л}Shg\]

Чтобы найти искомую работу \(A\) нужно построить график изменения силы \(F\) от перемещения \(x\). Площадь под графиком численно равна работе \(A\).

При \(x=0\) внешняя сила \(F\) также равна нулю (из-за равенства (1)):

\[F\left( 0 \right) = {\rho _в}gS{h_0} — {\rho _л}Shg = 0\]

При \(x=\left({h-h_0}\right)\), то есть когда льдина полностью погружена, сила \(F\) будет равна:

\[F\left( {h — {h_0}} \right) = {\rho _в}gSh — {\rho _л}Shg = \left( {{\rho _в} — {\rho _л}} \right)Sgh\]

График приведен на схеме. Посчитаем работу, как площадь треугольника под графиком функции:

\[A = \frac{1}{2}\left( {{\rho _в} — {\rho _л}} \right)Sgh \cdot \left( {h — {h_0}} \right)\]

Учитывая (2), получим:

\[A = \frac{1}{2}\left( {{\rho _в} — {\rho _л}} \right)Sgh \cdot \left( {h — \frac{{{\rho _л}}}{{{\rho _в}}}h} \right)\]

\[A = \frac{1}{2}\left( {{\rho _в} — {\rho _л}} \right)Sg{h^2} \cdot \left( {1 — \frac{{{\rho _л}}}{{{\rho _в}}}} \right)\]

Плотность льда \(\rho_{л}\) равна 900 кг/м³, плотность воды \(\rho_{в}\) равна 1000 кг/м³. Посчитаем ответ:

\[A = \frac{1}{2}\left( {1000 — 900} \right) \cdot 5 \cdot 10 \cdot {0,5^2} \cdot \left( {1 — \frac{{900}}{{1000}}} \right) = 62,5\;Дж\]

Ответ: 62,5 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.45 Шарик от настольного тенниса диаметром 4 см и массой 8 г удерживается под водой
3.3.47 Однородный куб плавает в воде, на 0,75 своего объема погрузившись в воду. Если
3.3.48 Однородный пробковый брусок квадратного сечения со стороной 10 см и длиной 40 см