Условие задачи:

В ящике находится шар массой 3 кг. Ящик наклоняют так, что его дно составляет с горизонтом угол 30°. Определить модуль силы давления шара на дно ящика.

Задача №3.1.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=3\) кг, \(\alpha=30^\circ\), \(F-?\)

Решение задачи:

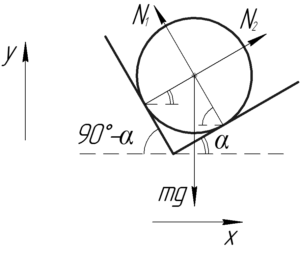Изобразим на схеме шар в ящике, при этом будем считать, что стенки ящика образуют с его дном прямой угол. На шар действуют следующие силы: сила тяжести и две силы нормальной реакции со стороны дна и стенки ящика. Шар покоится, применим первое условие равновесия в проекции на оси \(x\) и \(y\).

\[\left\{ \begin{gathered}
{N_2} \cdot \cos \alpha = {N_1} \cdot \cos \left( {90^\circ — \alpha } \right) \hfill \\
{N_2} \cdot \sin \alpha + {N_1} \cdot \sin \left( {90^\circ — \alpha } \right) = mg \hfill \\
\end{gathered} \right.\]

Так как \(\sin \alpha  = \cos \left( {90^\circ  — \alpha } \right)\) и \(\cos \alpha  = \sin \left( {90^\circ  — \alpha } \right)\), то:

\[\left\{ \begin{gathered}
{N_2} \cdot \cos \alpha = {N_1} \cdot \sin \alpha \;\;\;\;(1)\hfill \\
{N_2} \cdot \sin \alpha + {N_1} \cdot \cos \alpha = mg \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Из равенства (1) выразим силу нормальной реакции \(N_2\) со стороны стенки ящика:

\[{N_2} = {N_1} \cdot tg\alpha \]

Полученное выражение подставим в (2), тогда:

\[{N_1} \cdot tg\alpha  \cdot \sin \alpha  + {N_1} \cdot \cos \alpha  = mg\]

\[{N_1}\left( {tg\alpha  \cdot \sin \alpha  + \cos \alpha } \right) = mg\]

\[{N_1} = \frac{{mg}}{{tg\alpha  \cdot \sin \alpha  + \cos \alpha }}\]

Сила давления \(F\) равна по модулю силе реакции \(N_1\) согласно третьему закону Ньютона.

\[F = {N_1}\]

\[F = \frac{{mg}}{{tg\alpha  \cdot \sin \alpha  + \cos \alpha }}\]

Домножим и числитель, и знаменатель на \(\cos \alpha\):

\[F = \frac{{mg \cdot \cos \alpha }}{{{{\sin }^2}\alpha {\text{}} + {{\cos }^2}\alpha }}\]

\[F = mg \cdot \cos \alpha \]

Подставим данные задачи в формулу и посчитаем ответ:

\[F = 3 \cdot 10 \cdot \cos 30^\circ = 26\;Н\]

Прошу не игнорировать информацию о том, что задачу можно решить гораздо быстрее, выбрав направление осей x и y вдоль стенок ящика (за ценный комментарий спасибо Анастасии).

Ответ: 26 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.9 Шар массой 5 кг опирается на две гладкие плоскости, образующие угол, причем
3.1.11 На двух взаимно перпендикулярных наклонных плоскостях, из которых одна наклонена
3.1.12 При подвеске контактного провода троллейбусной сети провес опорного троса