Условие задачи:
В закрепленной металлической сфере радиусом 1 см, имеющей заряд -10 нКл, проделано очень маленькое отверстие. Точечный заряд 1 нКл массой 1 мг летит по прямой, проходящей через центр сферы и отверстие, имея на очень большом расстоянии от сферы скорость 1 м/с. Какова скорость этого заряда в центре сферы?
Задача №6.3.54 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R=1\) см, \(Q=-10\) нКл, \(q=1\) нКл, \(m=1\) мг, \(\upsilon_0=1\) м/с, \(\upsilon-?\)
Решение задачи:
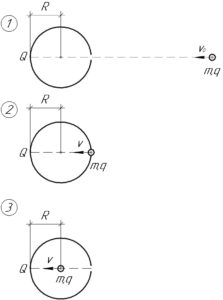 Поскольку внутри заряженной сферы поле отсутствует, значит на электрон при нахождении внутри сферы не будут оказывать действие никакие силы. Получается, что по первому закону Ньютона, в центре сферы электрон будет иметь такую же скорость, что и при влёте в сферу (изображение 3 на схеме).
Поскольку внутри заряженной сферы поле отсутствует, значит на электрон при нахождении внутри сферы не будут оказывать действие никакие силы. Получается, что по первому закону Ньютона, в центре сферы электрон будет иметь такую же скорость, что и при влёте в сферу (изображение 3 на схеме).
Поскольку сфера и точечный заряд имеют разноимённые заряды, то понятно, что они будут притягиваться. В начале (изображение 1), когда точечный заряд находился на очень большом расстоянии от сферы, энергия системы «сфера — точечный заряд» \(W_0\) была равна начальной кинетической энергии точечного заряда, которую можно определить из формулы:
\[{W_0} = \frac{{m\upsilon _0^2}}{2}\]
Когда точечный заряд «достигнет» поверхности сферы (точнее окажется на расстоянии \(R\) от центра сферы, ведь достигнуть он её не может, поскольку там отверстие (изображение 2)), энергия системы «сфера — точечный заряд» \(W\) станет равной сумме кинетической энергии точечного заряда и потенциальной энергии взаимодействия зарядов сферы и точечного заряда, т.е:
\[W = \frac{{m{\upsilon ^2}}}{2} + \frac{{kQq}}{R}\]
Поскольку на систему не действуют внешние силы, значит выполняется закон сохранения энергии, то есть:
\[{W_0} = W\]
\[\frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + \frac{{kQq}}{R}\]
Откуда можно выразит искомую скорость \(\upsilon\):
\[\upsilon = \sqrt {\upsilon _0^2 — \frac{{2kQq}}{{mR}}} \]
Произведём расчёты:
\[\upsilon = \sqrt {{1^2} — \frac{{2 \cdot 9 \cdot {{10}^9} \cdot \left( { — 10 \cdot {{10}^{ — 9}}} \right) \cdot 1 \cdot {{10}^{ — 9}}}}{{1 \cdot {{10}^{ — 6}} \cdot 0,01}}} = 4,36\;м/с\]
Ответ: 4,36 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.53 В электронно-лучевой трубке поток электронов с кинетической энергией 8 кэВ
6.3.55 В зазор между пластинами плоского конденсатора влетает электрон, пройдя перед
6.3.56 Неподвижно закрепленный шарик, заряженный положительно, находится над шариком

 icodepro.ru
icodepro.ru
В закрепленной металлической сфере радиуса r = 10^-2 м, имеющей заряд q1 = -10^-8 Кл, проделано очень маленькое отверстие. Точечный заряд q2 = 10^-9 Кл массы m = 10^-6 кг летит по прямой, проходящей через центр сферы и отверстие, имея на очень большом расстоянии от сферы скорость v0 = 1 м/с. Какова скорость v точечного заряда в центре сферы?