Условие задачи:
В зазор между пластинами плоского конденсатора влетает электрон, пройдя перед этим ускоряющее поле с разностью потенциалов 25 кВ. Скорость электрона направлена параллельно пластинам конденсатора. Длина пластин 8 см, расстояние между ними 1 см. На сколько сместится электрон при выходе из зазора между пластинами, если разность потенциалов между ними 200 В?
Задача №6.3.55 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\Delta \varphi = 25\) кВ, \(l=8\) см, \(d=1\) см, \(U=200\) В, \(\delta-?\)
Решение задачи:
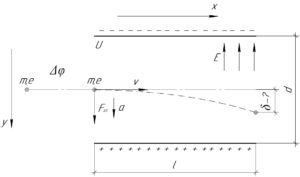 При нахождении электрона между обкладками конденсатора на него вдоль оси \(y\) действует электрическая сила \(F_{эл}\), модуль которой мы найдём по формуле:
При нахождении электрона между обкладками конденсатора на него вдоль оси \(y\) действует электрическая сила \(F_{эл}\), модуль которой мы найдём по формуле:
\[F_{эл} = Ee\]
В этой формуле \(e\) — модуль заряда электрона (элементарный заряд), равный 1,6·10-19 Кл.
Напряженность поля конденсатора \(E\) можно выразить через разность потенциалов между пластинами \(U\) (или его ещё называют напряжением) и расстояние между ними \(d\):
\[E = \frac{U}{d}\]
Тогда:
\[{F_{эл}} = \frac{{Ue}}{d}\;\;\;\;(1)\]
Запишем второй закон Ньютона для электрона в проекции на ось \(y\):
\[{F_{эл}} = ma\;\;\;\;(2)\]
Здесь \(m\) — масса электрона, равная 9,1·10-31 кг. Приравняем (1) и (2), тогда:
\[\frac{{Ue}}{d} = ma\]
Давайте выразим из полученного равенства ускорение электрона \(a\), оно ещё нам пригодится:
\[a = \frac{{Ue}}{{md}}\;\;\;\;(3)\]
Теперь запишем уравнения движения электрона вдоль осей координат. Вдоль оси \(x\) электрон движется равномерно (так как вдоль этой оси на него не действуют силы), а вдоль оси \(y\) — равноускоренно (из-за электрической силы \(F_{эл}\)) без начальной скорости.
\[\left\{ \begin{gathered}
x = \upsilon t \hfill \\
y = \frac{{a{t^2}}}{2} \hfill \\
\end{gathered} \right.\]
Пусть \(t\) — время нахождения электрона в конденсаторе. За это время электрон вдоль оси \(x\) пройдёт путь, равный длине обкладок \(l\), а вдоль оси \(y\) — путь, равный смещению пучка \(\delta\), поэтому вышеприведённая система примет вид:
\[\left\{ \begin{gathered}
l = \upsilon t \hfill \\
\delta = \frac{{a{t^2}}}{2} \hfill \\
\end{gathered} \right.\]
Из верхнего уравнения выразим время движения \(t\) и возведём его в квадрат:
\[t = \frac{l}{\upsilon } \Rightarrow {t^2} = \frac{{{l^2}}}{{{\upsilon ^2}}}\;\;\;\;(4)\]
В нижнее уравнение системы подставим (3) и (4), тогда:
\[\delta = \frac{{eU{l^2}}}{{2md{\upsilon ^2}}}\;\;\;\;(5)\]
В условии задачи сказано, что электрон был ускорен разностью потенциалов \(\Delta \varphi\), поэтому, записав закон сохранения энергии, мы легко можем определить скорость электрона \(\upsilon\) при влёте в конденсатор (вернее нам нужен квадрат скорости \(\upsilon^2\)).
\[e\Delta \varphi = \frac{{m{\upsilon ^2}}}{2}\]
\[{\upsilon ^2} = \frac{{2e\Delta \varphi }}{m}\]
Полученное выражение подставим в формулу (5):
\[\delta = \frac{{eU{l^2}}}{{2md}} \cdot \frac{m}{{2e\Delta \varphi }}\]
\[\delta = \frac{{U{l^2}}}{{4d\Delta \varphi }}\]
Задача решена, теперь нужно поставить численные значения величин и посчитать численный ответ:
\[\delta = \frac{{200 \cdot {{0,08}^2}}}{{4 \cdot 25 \cdot {{10}^3} \cdot 0,01}} = 0,00128\;м = 0,128\;см\]
Ответ: 0,128 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.54 В закрепленной металлической сфере радиусом 1 см, имеющей заряд -10 нКл
6.3.56 Неподвижно закрепленный шарик, заряженный положительно, находится над шариком
6.3.57 Заряды q1=2 мкКл и q2=5 мкКл расположены на расстоянии AB=40 см друг от друга

 icodepro.ru
icodepro.ru