Условие задачи:
Велосипедист, имея начальную скорость 2 м/с, спускается с горы с ускорением 0,4 м/с2 в течение 8 с. Чему равна скорость велосипедиста в конце пути?
Задача №1.3.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=2\) м/с, \(a=0,4\) м/с2, \(t=8\) с, \(\upsilon-?\)
Решение задачи:
Сделаем рисунок, на котором введем ось \(x\) вдоль склона горы и обозначим все необходимые величины.
Велосипедист, двигаясь под уклон, будет увеличивать свою скорость. Чтобы найти конечную скорость используем следующую формулу (ее называют формулой скорости):
\[\upsilon = {\upsilon _0} + at\]
Остается только подставить числа в формулу и сосчитать ответ.
\[\upsilon = 2 + 0,4 \cdot 8 = 5,2\; м/с = 18,72\; км/ч \]
Ответ: 18,72 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.5 За 2 с тело изменило скорость от 8 м/с до 24 м/с. С каким ускорением оно
1.3.7 Движение тела задано уравнением S=40t-0,2t^2. Через какое время
1.3.8 Тело, двигаясь равноускоренно, проходит 80 м за 4 с. Чему равна мгновенная

 icodepro.ru
icodepro.ru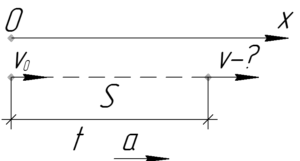
5,2 м/с = 18,72 км/ч это как?
Чтобы перевести из м/с в км/ч нужно умножить на 3,6. Вот почему:\[5,2\;м/с = \frac{{5,2 \cdot \frac{1}{{1000}}}}{{1 \cdot \frac{1}{{3600}}}} = \frac{{5,2 \cdot 3600}}{{1000}} = 5,2 \cdot 3,6 = 18,72\;км/ч\]Метр — это \(\frac{1}{1000}\) километра, а секунда — это \(\frac{1}{3600}\) часа