icodepro.ruУсловие задачи:
Во сколько раз изменится центростремительное ускорение тела, если оно будет двигаться равномерно по окружности вдвое большего радиуса с той же угловой скоростью?
Задача №1.8.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_2=2R_1\), \(\omega_1=\omega_2\), \(\frac{a_{ц2}}{a_{ц1}}-?\)
Решение задачи:
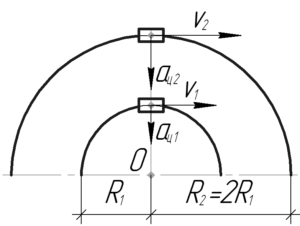Для начала напомним, что центростремительное ускорение \(a_ц\) связано с угловой скоростью \(\omega\) и радиусом \(R\) формулой:
\[a_ц = {\omega ^2}R\]
Тогда:
\[\frac{{{a_{ц2}}}}{{{a_{ц1}}}} = \frac{{\omega _2^2{R_2}}}{{\omega _1^2{R_1}}}\]
Так как по условию их угловые скорости равны, а радиус \(R_2\) в два раза больше \(R_1\), то:
\[\frac{{{a_{ц2}}}}{{{a_{ц1}}}} = \frac{{\omega _1^2 \cdot 2{R_1}}}{{\omega _1^2{R_1}}} = 2\]
Ответ: увеличится в 2 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.7 С какой скоростью автомобиль должен проходить середину выпуклого моста
1.8.9 Колесо велосипеда делает 100 об/мин. Каков радиус колеса, если скорость
1.8.10 Минутная стрелка часов в 3 раза длиннее секундной. Во сколько раз линейная скорость
Центростремительное ускорение имеют формулу U^2/R , тогда же оно уменьшится в два раза при увеличении знаменателя , как правильно?
Лучше использовать для сравнения формулу \(a_ц = {\omega ^2}R\), а не \(a_ц = \frac{{{\upsilon ^2}}}{R}\). Дело в том, что угловая скорость \(\omega\) точно одинакова для двух сравниваемых случаев (об этом сказано в условии). Линейная же скорость \(\upsilon\) зависит от радиуса (чем дальше от оси вращения, тем линейная скорость больше), который для двух сравниваемых случаев различен. Если Вы все-таки решите использовать свою формулу, то все равно дальше путем преобразований придете к \(a_ц = {\omega ^2}R\).