Условие задачи:

Во сколько раз изменится запас потенциальной энергии упруго деформированного тела при увеличении его деформации в 2 раза?

Задача №2.7.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$x_2=2x_1$, $\frac{E_{п2}}{E_{п1}}-?$

Решение задачи:

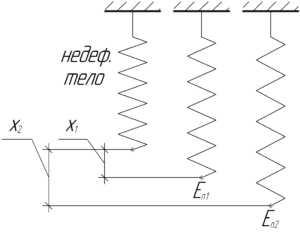Известно, что потенциальную энергию деформированного тела (например, пружины) можно найти по следующей формуле:

$${E_{п}} = \frac{{k{x^2}}}{2}$$

В задании говорится, что изначально тело было деформировано на величину $x_1$, а затем деформацию увеличивают до значения $x_2$, равного $2x_1$. Потенциальную энергию в этих состояниях найдем по формулам:

$$\left\{ \begin{gathered} {E_{п1}} = \frac{{kx_1^2}}{2} \hfill \\ {E_{п2}} = \frac{{kx_2^2}}{2} \hfill \\ \end{gathered} \right.$$

Найдем искомое отношение $\frac{E_{п2}}{E_{п1}}$, поделив нижнее равенство на верхнее:

$$\frac{{{E_{п2}}}}{{{E_{п1}}}} = \frac{{x_2^2}}{{x_1^2}}$$

По условию $x_2=2x_1$, поэтому:

$$\frac{{{E_{п2}}}}{{{E_{п1}}}} = \frac{{{{\left( {2{x_1}} \right)}^2}}}{{x_1^2}} = \frac{{4x_1^2}}{{x_1^2}} = 4$$

Ответ: увеличится в 4 раза.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.7.10 Санки тянут на пути 100 м с силой 80 Н за веревку, составляющую угол 30 градусов
2.7.12 При торможении автомобиля массой 1 т скорость уменьшилась от 72 км/ч до 36 км/ч
2.7.13 Автомобиль массой 1500 кг, двигаясь равноускоренно, проходит путь 20 м за 2 с