Условие задачи:
Вычислить путь, который проехал за 30 с велосипедист, двигающийся с угловой скоростью 0,10 рад/с по окружности радиуса 100 м.
Задача №1.8.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t=30\) с, \(\omega=0,10\) рад/с, \(R=100\) м, \(S-?\)
Решение задачи:
 Так как движение по окружности является равномерным, то путь \(S\), пройденный за время \(t\), найдется по формуле:
Так как движение по окружности является равномерным, то путь \(S\), пройденный за время \(t\), найдется по формуле:
\[S = \upsilon t\]
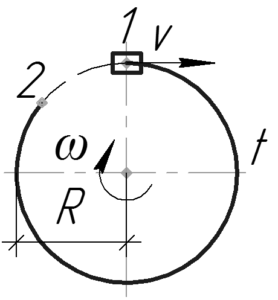
На рисунке путь велосипедиста по окружности показан выделенным, начальная точка пути — 1, конечная — 2.
В этой формуле \(\upsilon\) — это линейная скорость велосипедиста, её можно найти через угловую скорость \(\omega\) по формуле:
\[\upsilon = \omega R\]
В конечном счете для нахождения искомого пути необходимо применить формулу:
\[S = \omega Rt\]
Некоторые могут возмутиться простотой задачи и спросить, почему же при движении по окружности есть ускорение, и разве оно никак не влияет на пройденный путь? Ускорение при равномерном (и только таком) движении по окружности меняет скорость по направлению, а не по величине. Поэтому оно никак и не влияет на путь.
Численный значение пройденного пути равно:
\[S = 0,10 \cdot 100 \cdot 30 = 300\; м = 0,3\; км\]
Ответ: 0,3 км.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.17 Вертолет начал снижаться вертикально вниз с ускорением 0,2 м/с2. Лопасть винта
1.8.19 Материальная точка движется по окружности. Угол поворота радиуса, соединяющего
1.8.20 Найти радиус вращающегося колеса, если линейная скорость точки на ободе

 icodepro.ru
icodepro.ru
Классное решение