Условие задачи:

Высота Солнца над горизонтом 38°. Под каким углом к горизонту надо расположить плоское зеркало, чтобы осветить солнечными лучами дно вертикального колодца?

Задача №10.1.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=38^\circ\), \(\gamma-?\)

Решение задачи:

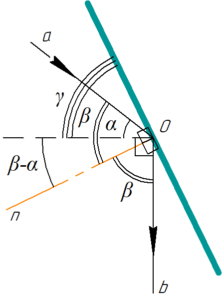Разумеется, для решения этой задачи (как и для решения любой задачи по оптике) необходимо сделать рисунок. Для начала Вам нужно провести под углом \(\alpha\) к горизонту луч a, а затем в некоторой точке O изменить его направление на вертикальное (как луч b на рисунке). Изменение направления распространения луча произойдет из-за отражения в зеркале в точке O, значит луч a — это падающий на зеркало луч, а луч b — это отраженный от зеркала луч. Угол между ними должен быть равен углу \(2\beta\), где \(\beta\) — луч падения (или отражения) луча. Поэтому, если мы проведем биссектрису между падающим и отраженным лучом, то найдем положение нормали n к зеркалу. Зная положение нормали, легко найти положение самого зеркала, оно перпендикулярно нормали и проходит через точку O. Кстати, на рисунке сразу прекрасно видно, что угол между горизонтом и нормалью к зеркалу n равен \(\left( {\beta — \alpha } \right)\), это понадобится нам в дальнейшем решении. Из рисунка видно, что:

\[2\beta = \alpha + 90^\circ \]

\[\beta = \frac{{\alpha + 90^\circ }}{2}\;\;\;\;(1)\]

Также благодаря рисунку можно сделать вывод, что:

\[\gamma + \left( {\beta — \alpha } \right) = 90^\circ \]

Учитывая (1), имеем:

\[\gamma + \left( {\frac{{\alpha + 90^\circ }}{2} — \alpha } \right) = 90^\circ \]

\[\gamma + \left( {\frac{{90^\circ — \alpha }}{2}} \right) = 90^\circ \]

\[\gamma = 90^\circ — \frac{{90^\circ — \alpha }}{2}\]

\[\gamma = \frac{{90^\circ + \alpha }}{2}\]

Посчитаем численный ответ задачи:

\[\gamma = \frac{{90^\circ + 38^\circ }}{2} = 64^\circ \]

Ответ: 64°.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.1.6 Над центром круглого бассейна радиусом 5 м, залитого до краев водой, висит лампа
10.1.8 Солнечный луч, проходящий через отверстие в ставне, составляет с поверхностью стола
10.1.9 Небольшой предмет расположен между двумя плоскими зеркалами, образующими угол