Условие задачи:
Ядро массой 8 кг, выпущенное метателем под углом 45° к горизонту с высоты 1,5 м, улетело по горизонтали на расстояние 18,5 м. Определить работу, совершенную при толкании ядра.
Задача №2.7.47 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=8\) кг, \(\alpha=45^\circ\), \(h=1,5\) м, \(S=18,5\) м, \(A-?\)
Решение задачи:
 Искомая работа \(A\), совершенная метателем при толкании ядра, равна изменению кинетической энергии ядра согласно теореме об изменении кинетической энергии.
Искомая работа \(A\), совершенная метателем при толкании ядра, равна изменению кинетической энергии ядра согласно теореме об изменении кинетической энергии.
\[A = \frac{{m\upsilon _0^2}}{2}\;\;\;\;(1)\]
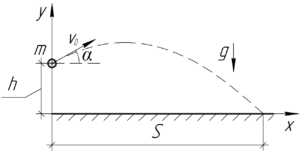
В этой формуле нам неизвестна скорость \(\upsilon\). Попробуем найти её, записав законы движения ядра в проекции на оси \(x\) и \(y\) (смотрите схему).
\[\left\{ \begin{gathered}
x = {\upsilon _0}\cos \alpha \cdot t \hfill \\
y = h + {\upsilon _0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2} \hfill \\
\end{gathered} \right.\]
Через время \(t\), равное времени полета ядра, его координата \(x\) станет равной \(S\), а координата \(y\) — нулю.
\[\left\{ \begin{gathered}
S = {\upsilon _0}\cos \alpha \cdot t \hfill \\
0 = h + {\upsilon _0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2} \hfill \\
\end{gathered} \right.\]
На этом физика в этой задаче закончилась, осталось лишь математика. Из верхнего равенства выразим время полета \(t\) и подставим его в нижнее равенство.
\[t = \frac{S}{{{\upsilon _0}\cos \alpha }}\]
\[0 = h + \frac{{S \cdot {\upsilon _0}\sin \alpha }}{{{\upsilon _0}\cos \alpha }} — \frac{g}{2} \cdot \frac{{{S^2}}}{{\upsilon _0^2{{\cos }^2}\alpha }}\]
Выразим из полученного квадрат скорости \({\upsilon}^2\).
\[0 = h + S \cdot tg\alpha — \frac{{g{S^2}}}{{2\upsilon _0^2{{\cos }^2}\alpha }}\]
\[\frac{{g{S^2}}}{{2\upsilon _0^2{{\cos }^2}\alpha }} = h + S \cdot tg\alpha \]
\[\upsilon _0^2 = \frac{{g{S^2}}}{{2{{\cos }^2}\alpha \left( {h + S \cdot tg\alpha } \right)}}\]
Полученное выражение подставим в формулу (1), так мы получим решение задачи в общем виде:
\[A = \frac{{mg{S^2}}}{{4{{\cos }^2}\alpha \left( {h + S \cdot tg\alpha } \right)}}\]
Теперь посчитаем численный ответ:
\[A = \frac{{8 \cdot 10 \cdot {{18,5}^2}}}{{4 \cdot {{\cos }^2}45^\circ \cdot \left( {1,5 + 18,5 \cdot tg45^\circ } \right)}} = 684,5\;Дж\]
Ответ: 684,5 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.46 Трактор массой 10 т и мощностью 150 кВт поднимается в гору со скоростью 5 м/с
2.7.48 Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна
2.7.49 Конькобежец движется по горизонтальному пути равномерно, а затем с разгона проезжает

 icodepro.ru
icodepro.ru
Изменение кинетической энергии: mv2/2-mv02/2 почему формула тогда просто mv2/2?
Подскажите, пожалуйста
Потому что начальная скорость ядра \(\upsilon_0\) равна нулю (когда ядро находится с руках метателя перед броском).