Условие задачи:
За седьмую секунду равноускоренного движения модуль вектора скорости увеличился на 1,4 м/с. На сколько увеличился вектор модуль вектора скорости тела за первые две секунды движения?
Задача №1.3.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\Delta \upsilon_1=1,4\) м/с, \(\Delta t_1=1\) с, \(\Delta t_2=2\) с, \(\Delta \upsilon_2-?\)
Решение задачи:
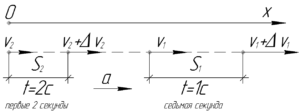 Равноускоренное прямолинейное (и только такое!) движение — это движение тела, при котором за равные промежутки времени скорость тела возрастает на одинаковую величину. Поэтому неважно за какую секунду — за седьмую или за первую — а важно что за одну секунду!
Равноускоренное прямолинейное (и только такое!) движение — это движение тела, при котором за равные промежутки времени скорость тела возрастает на одинаковую величину. Поэтому неважно за какую секунду — за седьмую или за первую — а важно что за одну секунду!
После этих рассуждений ответ в принципе очевиден, если за одну (седьмую) секунду тело ускорилось на 1,4 м/с, то за первые две секунды — на 2,8 м/с. Но давайте покажем наши мысли на языке математики.
\[\left\{ \begin{gathered}
\Delta {\upsilon _1} = a{t_1} \hfill \\
\Delta {\upsilon _2} = a{t_2} \hfill \\
\end{gathered} \right.\]
Поделим нижнее выражение на верхнее и выразим искомую \(\Delta \upsilon_2\).
\[\frac{{\Delta {\upsilon _2}}}{{\Delta {\upsilon _1}}} = \frac{{{t_2}}}{{{t_1}}} \Rightarrow \Delta {\upsilon _2} = \Delta {\upsilon _1}\frac{{{t_2}}}{{{t_1}}}\]
\[\Delta {\upsilon _2} = 1,4\frac{2}{1} = 2,8\; м/с = 10,1\; км/ч\]
Ответ: 10,1 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.31 За первую секунду равноускоренного движения тело проходит путь 1 м, а за
1.3.33 К концу первой секунды равнозамедленного движения модуль скорости тела
1.3.34 На некотором отрезке пути скорость тела увеличилась с 12 см/с до 16 см/с

 icodepro.ru
icodepro.ru
Мне кажется, или в условии написано за седьмую секунду?
упс, понял свою ошибку, начало решения не прочитал)