Условие задачи:
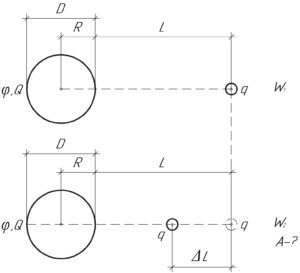
Заряд 5 нКл находится на расстоянии 0,45 м от поверхности шара диаметром 0,1 м, заряженного до потенциала 2400 В. Какую работу надо совершить, чтобы уменьшить расстояние между зарядов и шаром на 0,4 м?
Задача №6.3.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q=5\) нКл, \(L=0,45\) м, \(D=0,1\) м, \(\varphi=2400\) В, \(\Delta L=0,4\) м, \(A-?\)
Решение задачи:
 Зная потенциал \(\varphi\), до которого заряжен шар, мы можем определить его заряд \(Q\). Для этого сначала запишем формулу для определения потенциала шара, а далее уже оттуда выразим заряд:
Зная потенциал \(\varphi\), до которого заряжен шар, мы можем определить его заряд \(Q\). Для этого сначала запишем формулу для определения потенциала шара, а далее уже оттуда выразим заряд:
\[\varphi = \frac{{kQ}}{R}\]
В этой формуле \(k\) — коэффициент пропорциональности (из закона Кулона), равный 9·109 Н·м2/Кл2. Так как радиус шара \(R\) равен половине диаметра \(D\), то есть \(R=\frac{D}{2}\), то:
\[\varphi = \frac{{2kQ}}{D}\]
\[Q = \frac{{\varphi D}}{{2k}}\;\;\;\;(1)\]
Так как шар и заряд заряжены одноимённо, то для их сближения придётся внешней силой совершить работу, которую можно найти как изменение потенциальной энергии системы «шар-заряд». Поэтому:
\[A = {W_2} — {W_1}\]
Теперь необходимо расписать по формулам начальную и конечную потенциальные энергии \(W_1\) и \(W_2\), при этом расстояния необходимо расписывать от центра шара до заряда.
\[A = \frac{{kQq}}{{\frac{D}{2} + L — \Delta L}} — \frac{{kQq}}{{\frac{D}{2} + L}}\]
Домножим числитель и знаменатель дробей в правой части на 2:
\[A = \frac{{2kQq}}{{D + 2L — 2\Delta L}} — \frac{{2kQq}}{{D + 2L}}\]
Также в правой части приведём под общий знаменатель:
\[A = \frac{{2kQq\left( {D + 2L} \right) — 2kQq\left( {D + 2L — 2\Delta L} \right)}}{{\left( {D + 2L — 2\Delta L} \right)\left( {D + 2L} \right)}}\]
\[A = \frac{{4kQq\Delta L}}{{\left( {D + 2L — 2\Delta L} \right)\left( {D + 2L} \right)}}\]
Учтём ранее полученную формулу (1):
\[A = \frac{{4kq\Delta L}}{{\left( {D + 2L — 2\Delta L} \right)\left( {D + 2L} \right)}} \cdot \frac{{\varphi D}}{{2k}}\]
\[A = \frac{{2q\Delta L\varphi D}}{{\left( {D + 2L — 2\Delta L} \right)\left( {D + 2L} \right)}}\]
Поздравляем, задача решена. Подставим численные значения величин в формулу и посчитаем численный ответ:
\[A = \frac{{2 \cdot 5 \cdot {{10}^{ — 9}} \cdot 0,4 \cdot 2400 \cdot 0,1}}{{\left( {0,1 + 2 \cdot 0,45 — 2 \cdot 0,4} \right)\left( {0,1 + 2 \cdot 0,45} \right)}} = 4,8 \cdot {10^{ — 6}}\;Дж = 4,8\;мкДж\]
Ответ: 4,8 мкДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.44 Какую скорость может сообщить электрону, находящемуся в состоянии покоя
6.3.46 Два электрона движутся под действием сил электростатического отталкивания
6.3.47 Между катодом и анодом двухэлектродной лампы приложена разность потенциалов

 icodepro.ru
icodepro.ru
спс


рахмет