Условие задачи:
 Заряды \(q_1=2\) мкКл и \(q_2=5\) мкКл расположены на расстоянии AB=40 см друг от друга. Определить абсолютную величину работы электрических сил при перемещении заряда \(q=10\) нКл из точки C в точку D, если AC=30 см.
Заряды \(q_1=2\) мкКл и \(q_2=5\) мкКл расположены на расстоянии AB=40 см друг от друга. Определить абсолютную величину работы электрических сил при перемещении заряда \(q=10\) нКл из точки C в точку D, если AC=30 см.
Задача №6.3.57 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q_1=2\) мкКл, \(q_2=5\) мкКл, \(a=40\) см, \(q=10\) нКл, \(b=30\) см, \(A-?\)
Решение задачи:
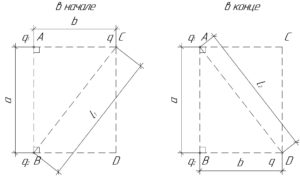 Работу электрических сил \(A\) можно найти как разность конечной \(W_2\) и начальной \(W_1\) суммарной потенциальной энергии взаимодействия трёх указанных зарядов, то есть:
Работу электрических сил \(A\) можно найти как разность конечной \(W_2\) и начальной \(W_1\) суммарной потенциальной энергии взаимодействия трёх указанных зарядов, то есть:
\[A = {W_2} — {W_1}\;\;\;\;(1)\]
Сначала определим конечную потенциальную энергию взаимодействия зарядов \(W_2\), для чего определимся с расстояниями между зарядами. В конце расстояние между зарядами \(q_1\) и \(q_2\) будет равно \(a\), между \(q_2\) и \(q\) — \(b\), а расстояние \(l_2\) между \(q_1\) и \(q\) можно найти по теореме Пифагора:
\[{l_2} = \sqrt {{a^2} + {b^2}} \]
Поэтому потенциальную энергию взаимодействия зарядов \(W_2\) следует искать по формуле:
\[{W_2} = \frac{{k{q_1}{q_2}}}{a} + \frac{{k{q_2}q}}{b} + \frac{{k{q_1}q}}{{\sqrt {{a^2} + {b^2}} }}\;\;\;\;(2)\]
Напомним, что \(k\) — коэффициент пропорциональности (в законе Кулона), равный 9·109 Н·м2/Кл2.
Изначально расстояние между зарядами \(q_1\) и \(q_2\) было также равно \(a\), между \(q_1\) и \(q\) — \(b\), а расстояние \(l_1\) между \(q_2\) и \(q\) можно найти аналогично по теореме Пифагора:
\[{l_1} = \sqrt {{a^2} + {b^2}} \]
Значит начальную потенциальную энергию взаимодействия зарядов \(W_1\) определим по формуле:
\[{W_1} = \frac{{k{q_1}{q_2}}}{a} + \frac{{k{q_1}q}}{b} + \frac{{k{q_2}q}}{{\sqrt {{a^2} + {b^2}} }}\;\;\;\;(3)\]
Подставим (2) и (3) в (1), тогда:
\[A = \frac{{k{q_1}{q_2}}}{a} + \frac{{k{q_2}q}}{b} + \frac{{k{q_1}q}}{{\sqrt {{a^2} + {b^2}} }} — \frac{{k{q_1}{q_2}}}{a} — \frac{{k{q_1}q}}{b} — \frac{{k{q_2}q}}{{\sqrt {{a^2} + {b^2}} }}\]
\[A = \frac{{k{q_2}q}}{b} + \frac{{k{q_1}q}}{{\sqrt {{a^2} + {b^2}} }} — \frac{{k{q_1}q}}{b} — \frac{{k{q_2}q}}{{\sqrt {{a^2} + {b^2}} }}\]
\[A = \frac{{kq\left( {{q_2} — {q_1}} \right)}}{b} — \frac{{kq\left( {{q_2} — {q_1}} \right)}}{{\sqrt {{a^2} + {b^2}} }}\]
\[A = kq\left( {{q_2} — {q_1}} \right)\left( {\frac{1}{b} — \frac{1}{{\sqrt {{a^2} + {b^2}} }}} \right)\]
Отлично, у нас получилось решить эту задачу в общем виде. Осталось только подставить данные задачи в полученную формулу и посчитать ответ:
\[A = 9 \cdot {10^9} \cdot 10 \cdot {10^{ — 9}} \cdot \left( {5 \cdot {{10}^{ — 6}} — 2 \cdot {{10}^{ — 6}}} \right)\left( {\frac{1}{{0,3}} — \frac{1}{{\sqrt {{{0,4}^2} + {{0,3}^2}} }}} \right) = 0,00036\;Дж = 360\;мкДж\]
Ответ: 360 мкДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.56 Неподвижно закрепленный шарик, заряженный положительно, находится над шариком
6.3.58 Шарик массой 10 г с зарядом 100 мкКл подвешен на тонкой нити длиной 50 см
6.3.59 Внутри шарового металлического слоя, внутренний и внешний радиусы которого

 icodepro.ru
icodepro.ru