Условие задачи:
Заряженная частица, пройдя ускоряющую разность потенциалов 600 кВ, приобрела скорость 5400 км/с. Определить массу частицы, если её заряд равен \(2e\).
Задача №6.3.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\Delta \varphi = 600\) кВ, \(\upsilon=5400\) км/с, \(q=2e\), \(m-?\)
Решение задачи:
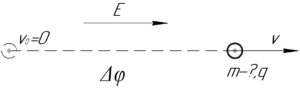 В условии задачи упомянута величина \(e\) — это модуль заряда электрона, который равен 1,6·10-19 Кл. Получается, что заряженная частица имеет положительный заряд.
В условии задачи упомянута величина \(e\) — это модуль заряда электрона, который равен 1,6·10-19 Кл. Получается, что заряженная частица имеет положительный заряд.
При прохождении частицей разности потенциалов поле совершит работу \(A\), которую можно определить по формуле:
\[A = \Delta \varphi \cdot q = 2\Delta \varphi e\;\;\;\;(1)\]
Также эту работу можно найти как изменение кинетической энергии частицы. Учитывая, что начальная скорость частицы равна нулю (это подразумевается), имеем:
\[A = \frac{{m{\upsilon ^2}}}{2}\;\;\;\;(2)\]
Теперь приравняем (1) и (2):
\[\frac{{m{\upsilon ^2}}}{2} = 2\Delta \varphi e\]
Откуда искомая масса \(m\) равна:
\[m = \frac{{4\Delta \varphi e}}{{{\upsilon ^2}}}\]
Посчитаем ответ к задаче:
\[m = \frac{{4 \cdot 600 \cdot {{10}^3} \cdot 1,6 \cdot {{10}^{ — 19}}}}{{{{\left( {5400 \cdot {{10}^3}} \right)}^2}}} = 1,32 \cdot {10^{ — 26}}\;кг\]
Ответ: 1,32·10-26 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.37 Между двумя горизонтально расположенными пластинами, заряженными до 10 кВ
6.3.39 Электрическое поле образовано двумя параллельными пластинами, находящимися
6.3.40 Пылинка массой 4×10^(-12) кг и зарядом 10^(-16) Кл попадает в поле заряженного

 icodepro.ru
icodepro.ru
А откуда взялось 10^3? И в числителе и в знаменателе.
Разность потенциалов дана в кВ, а в формулу мы должны подставить в В, поэтому в числителе появляется 10^3.
Аналогично, скорость дана в км/с, а в формулу мы должны подставить в м/с, поэтому в знаменателе в скобках появляется 10^3.
Спасибо большое!
электрон имеет положительный заряд ?)
Я написал «модуль заряда электрона», всё верно