В главе «Термодинамика» школьного курса физики имеется много задач, в которых рассматривается поведение простейшей термодинамической системы — идеального газа. Обычно эту систему представляют как достаточно разреженный газ, заключенный в цилиндре под поршнем (рис. 1). При этом термодинамика не рассматривает движения системы как целого и не учитывает потенциальной энергии системы во внешних силовых полях.
Напомним, что состояние идеального газа характеризуется следующими параметрами: давлением \(p\), объемом \(V\), температурой \(T\), массой \(m\) и молярной массой \(\mu\).
Говорит, что система находится в термодинамическом равновесии, если каждый параметр имеет одно и то же значение в любой точке объема системы. Например, газ, предоставленный самому себе, всегда распределяется равномерно по всему объему, так что давление всюду одно и то же. Такое состояние и соответствует равновесному. Если хотя бы один из параметров изменяется от точки к точке, то состояние системы неравновесное, в системе возможны различные процессы: диффузия, теплопередача и т. п. Равновесное состояние отличается от неравновесного тем, что в равновесном состоянии система может находиться сколь угодно долго, если, конечно, не меняются внешние условия.
Под влиянием внешних воздействий система переходит из одного состояния в другое. Изменение состояния системы называют процессом: процесс всегда связан с нарушением равновесия. Термодинамика рассматривает такие процессы, в которых начальное и конечное состояния являются равновесными. Но промежуточные состояния могут быть и неравновесными. Мы будем рассматривать наиболее простой случай, когда процесс происходит бесконечно медленно, так что состояние системы в любой момент можно считать равновесным. В таком случае говорят, что в системе происходит равновесный процесс, который представляет собой непрерывную последовательность равновесных состояний.
Понятия «равновесное состояние» и «равновесный процесс» являются, конечно, идеализацией, но идеализацией очень удобной для количественного анализа поведения системы.
Изменение одного из параметров влечет за собой изменение остальных параметров, поскольку все они связаны друг с другом. Взаимная зависимость между отдельными параметрами устанавливается экспериментально. Формулу, обобщающую результаты экспериментов, называют уравнением состояния системы. Для газов уравнение состояния (уравнение Клапейрона — Менделеева) имеет вид:
\(pV = \frac{m}{\mu }RT\) (1)
(\(R\) — универсальная газовая постоянная).
Равновесные состояния и равноценные процессы можно изображать графически. Для этого на двух взаимно перпендикулярных осях откладывают значения каких-либо двух параметров, например, давления \(p\) и объема \(V\), объема \(V\) и температуры \(T\), давления \(p\) и температуры \(T\). Таким образом получаются так называемые диаграммы состояния системы. На любой из диаграмм \(\left( {p,V} \right)\), \(\left( {V,T} \right)\) или \(\left( {p,T} \right)\) каждое равновесное состояние обозначается точкой, а равновесный процесс — линией.
В школьном курсе подробно рассматриваются три частных процесса: изотермический \(\left( {T = {\text{const}}} \right)\), изобарический \(\left( {p = {\text{const}}} \right)\) и изохорический \(\left( {V = {\text{const}}} \right)\) процессы, происходящие с газом неизменного химического состава \(\left( {\mu = {\text{const}}} \right)\) и постоянной массы \(\left( {m = {\text{const}}} \right)\). Соответствующие графики показаны на рисунке 2.
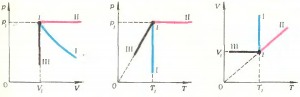
Но нельзя забывать, что в общем случае могут изменяться все без исключения параметры, в том числе \(m\) и \(\mu\). Пусть, например, газ переходит из состояния 1 (с параметрами \(p_1\), \(V_1\), \(T_1\), \(m_1\), \(\mu_1\)) в состояние 2 (с параметрами \(p_2\), \(V_2\), \(T_2\), \(m_2\), \(\mu_2\)). Вообще говоря, этот переход может быть осуществлен бесконечным числом способов, в зависимости от того, как меняются отдельные параметры. Например, на рисунке 3 изображены графики одного и того же процесса \(\left( {1 \to 2} \right)\) на различных диаграммах. Подумайте, как при этом изменяются масса и молярная масса газа.

Часто предметом беседы экзаменатора с абитуриентом становятся круговые процессы, или циклы. Цикл — это такой процесс, для которого совпадают начальное и конечное состояния. В качестве примера разберем такую задачу.
Задача 1
Как будет выглядеть график кругового процесса \(1 \to 2 \to 3 \to 4\) (рис. 4) на диаграмме \(\left( {p,V} \right)\)? Масса газа и его химический состав остаются неизменными.

Прежде всего «расшифруем» график, приведенный на диаграмме \(\left( {p,T} \right)\), и выясним, какие процессы проводились над газом?
На участке \(1 \to 2\) давление неизменно и имеет величину \(p_1\), а температура увеличивается от значения \(T_1\) до значения \(T_2\). Изменяться может лишь один параметр — объем \(V\). Следовательно, на первом этапе объем изобарически увеличивается от \(V_1\) до \(V_2\). На диаграмме \(\left( {p,V} \right)\) этот процесс изобразится прямой \(1 \to 2\), параллельной оси \(V\) (рис. 5).
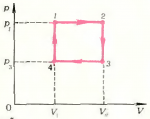
На участке \(2 \to 3\) давление изменяется прямо пропорционально температуре (прямая \(2 \to 3\) проходит через начало координат). Это указывает на то, что на этом участке объем газа не изменяется: \({V_2} = {V_3}\). На диаграмме \(\left( {p,V} \right)\) процесс \(2 \to 3\) изобразится вертикальным отрезком, идущим вниз, так как давление уменьшается.
Процесс \(3 \to 4\) — изобарический (\(p = {p_3}\)). Температура, а следовательно, и объем убывают. Процесс \(3 \to 4\) на диаграмме \(\left( {p,V} \right)\) будет изображаться отрезком, параллельным оси \(V\). Но пока остается неизвестным, где заканчивается процесс \(3 \to 4\), так как неизвестен объем \(V_4\). Поэтому предварительно исследуем процесс \(4 \to 1\). Из рисунка 4 видно, что в процессе \(4 \to 1\) давление растет прямо пропорционально абсолютной температуре. А это означает, что процесс происходит при \(\left( {V = {\text{const}}} \right)\), и \(V_4=V_1\). Окончательно график цикла \(1 \to 2 \to 3 \to 4\) на диаграмме \(\left( {p,V} \right)\) имеет вид, показанный на рисунке 5.
Умение строить графики круговых процессов иногда существенно облегчает количественные оценки некоторых характеристик этих процессов. Поясним это на двух конкретных задачах.
Задача 2
Над газом проводят два круговых процесса: процесс \(1 \to 2 \to 3 \to 1\) и процесс \(3 \to 4 \to 2 \to 3\). Графики этих процессов, представленные в координатах \(\left( {V,T} \right)\), изображены на рисунке 6. В каком случае газ совершит большую работу?

Решение этой задачи может быть сравнительно простым, если воспользоваться известным свойством диаграммы \(\left( {p,V} \right)\): работа, совершенная газом за цикл, пропорциональна площади фигуры, ограниченной графиком этого процесса. Значит, нам необходимо построить графики заданных круговых процессов на диаграмме \(\left( {p,V} \right)\).
Нетрудно видеть, что цикл \(1 \to 2 \to 3 \to 1\) состоит из процесса изохорического нагревания \(1 \to 2\), изотермического расширения \(2 \to 3\) и изобарического охлаждения \(3 \to 1\). В координатах \(\left( {p,V} \right)\) он принимает вид, показанный на рисунке 7.

Цикл \(3 \to 4 \to 2 \to 3\) состоит из процессов изохорического нагревания \(3 \to 4\), изобарического охлаждения \(4 \to 2\) и изотермического расширения \(2 \to 3\). Так как процессы \(2 \to 3\) для обоих циклов совпадают, то разумно графики зависимости \(p\left( V \right)\) дли них изобразить на одних осях координат (рис. 7).
Совершенно очевидно, что площадь фигуры \(1 \to 2 \to 3 \to 1\) меньше площади фигуры \(3 \to 4 \to 2 \to 3\). Отсюда непосредственно следует, что по модулю работа газа \(A\) в первом процессе меньше, чем во втором, т. е. \(\left| {{A_{1 \to 2 \to 3 \to 4}}} \right| < \left| {{A_{3 \to 4 \to 2 \to 3}}} \right|\). Но нельзя забывать, что работа, совершаемая газом, является алгебраической величиной: если процесс происходит с увеличением объема, то \(A > 0\), а если объем системы уменьшается, то \(A < 0\). Для круговых процессов можно сформулировать такое правило определения знака работы, совершенной газом: если обход контура кругового процесса совершается по часовой стрелке, то \(A > 0\); если же обход контура происходит против часовой стрелки, то \(A < 0\). Применив это правило к данной задаче, получаем:
\({A_{1 \to 2 \to 3 \to 4}} > 0\) и \({A_{3 \to 4 \to 2 \to 3}} < 0\).
Окончательно ответ задачи можно дать такой:
\({A_{1 \to 2 \to 3 \to 4}} > {A_{3 \to 4 \to 2 \to 3}}\),
но при этом
\(\left| {{A_{1 \to 2 \to 3 \to 4}}} \right| < \left| {{A_{3 \to 4 \to 2 \to 3}}} \right|\).
Задача 3
Газ совершает цикл \(1 \to 2 \to 3 \to 4 \to 1\) (рис. 8), состоящий из двух изотерм (\(1 \to 2\) и \(3 \to 4\)) и двух адиабат (\(2 \to 3\) и \(4 \to 1\)). Какие из этих процессов происходят при подведении теплоты к системе, а какие требуют отвода теплоты?
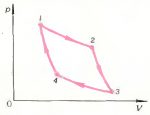
Учащиеся редко дают правильный ответ на этот вопрос. Наиболее распространенная ошибка заключается в том, что отождествляются два различных понятия: температура и количество теплоты. При этом утверждается, что если температура неизменна (процессы \(1 \to 2\) и \(3 \to 4\)), то теплоту не нужно ни подводить, ни отводить. Это, конечно, неверно.
Для решения задачи воспользуемся первым законом термодинамики:
\(Q = \Delta U + A\) (2)
Здесь \(Q\) — количество теплоты, переданное системе, \(\Delta U\) — изменение внутренней энергии системы и \(A\) — работа, совершенная системой.
Внутренняя энергия идеальною газа зависит лишь от температуры (конечно, при условии, что \(\left( {m = {\text{const}}} \right)\) и \(\left( {\mu = {\text{const}}} \right)\)). Поэтому для изотермического процесса \(1 \to 2\) изменение внутренней энергии \(\Delta U = 0\), и равенство (2) принимает вид:
\(Q = A\)
Так как объем системы увеличивается, то \(A > 0\). Следовательно, и \(Q > 0\), то есть к системе нужно подвести некоторое количество теплоты. За счет подведенной теплоты система и совершает работу в процессе изотермического расширения. Аналогичные рассуждения можно провести для процесса изотермического сжатия \(3 \to 4\). Но в этом случае объем системы уменьшается, поэтому \(A < 0\), и \(Q < 0\): теплоту нужно от системы отводить.
Процессы \(2 \to 3\) и \(4 \to 1\) адиабатные. По определению адиабатный процесс — это процесс без теплообмена с окружающей средой, то есть \(Q = 0\). Следовательно, на участках \(2 \to 3\) и \(4 \to 1\) теплота ни подводится к системе, ни отводится от нее.
Заметим, что адиабаты на диаграмма \(\left( {p,V} \right)\) идут круче, чем изотермы Это легко понять, если снова воспользоваться первым законом термодинамики, записанным для адиабатных процессов:
\(\Delta U + A = 0\).
При адиабатном расширении (процесс \(2 \to 3\)) система совершает работу за счет внутренней энергии:
\(A > 0\), и \(\Delta U < 0\).
Внутренняя энергия газа уменьшается и температура системы понижается (система переходит с изотермы \(1 \to 2\) на изотерму \(4 \to 3\), соответствующую более низкой температуре). При адиабатном сжатии (процесс \(4 \to 1\)):
\(A < 0\), и \(\Delta U > 0\).
Внутренняя энергия увеличивается, температура газа повышается.
Упражнения
1. На диаграмме (рис. 9) изображены изотермы для двух различных систем идеального газа. Чем различаются параметры этих систем?

2. На рисунке 10 дан график изменения состояния идеального газа в координатах \(\left( {p,V} \right)\). Представить этот круговой процесс на диаграмме \(\left( {V,T} \right)\).
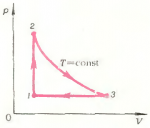
3. Над газом, масса которого \(m\), а молярная масса \(\mu\), производят круговой процесс \(1 \to 2 \to 3 \to 4 \to 1\), изображенный на рисунке 11. Температуры газа в состояниях 1, 2, 3 и 4 равны соответственно \(T_1\), \(T_2\), \(T_3\) и \(T_4\). Определить работу, совершенную газом за цикл.
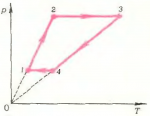
4. Изменение состояния газа при круговом процессе показано на анаграмме \(\left( {V,T} \right)\) (рис. 12). В каких процессах газ получает теплоту, а в каких отдает ее? Изобразите процесс на диаграмме \(\left( {p,T} \right)\).

Источник: Журнал “Квант”, №3 1976 г. Авторы: А. Диденко, Г. Дубровский.

Встречаются с адекватными и порядочными мужчинами, лучшие шлюхи Тверь, для обоюдно приятного времяпрепровождения с комфортом в тихой и уютной обстановке. Лучшие в городе лучшие шлюхи Тверь, страстные и желанные, они такие весёлые и молоденькие, что удовольствие неизбежно. Не отказывай себе в удовольствии.
 icodepro.ru
icodepro.ru
осталось добавить все разделы физики и будет лучший сайт, ведь тогда для изучения физики будет достаточно одного лишь вашего сайта

Спасибо!

Да, планируется ещё добавить теорию и статей по физике по всем разделам.