Решение: Колодец, имеющий глубину 5 м, площадь дна 0,5 м2, наполовину заполнен водой

Условие задачи:

Колодец, имеющий глубину 5 м, площадь дна 0,5 м², наполовину заполнен водой. Насос выкачивает воду и подает её на поверхность земли через цилиндрическую трубу радиусом 1,25 см. Какую работу совершит насос, если он выкачает всю воду из колодца за 5 мин?

Задача №2.8.46 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(H=5\) м, \(S=0,5\) м², \(r=1,25\) см, \(t=5\) мин, \(A-?\)

Решение задачи:

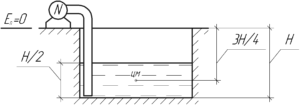Работа насоса заключается в изменении потенциальной и кинетической энергии всей воды, содержащейся в колодце.

\[A = \Delta {E_п} + \Delta {E_к}\;\;\;\;(1)\]

Но для начала давайте определим массу всей воды, которая имеется в колодце — её можно найти как произведение плотности воды (она равна 1000 кг/м³) на её объем.

\[m = \rho V\]

Поскольку колодец заполнен на половину, то объем воды найдем по формуле:

\[V = S\frac{H}{2}\;\;\;\;(2)\]

В итоге масса воды равна:

\[m = \rho S\frac{H}{2}\;\;\;\;(3)\]

Начальное положение центра масс всего объема воды находится на расстоянии \(\frac{3H}{4}\) от верхнего основания. Возьмем уровень нуля потенциальной энергии на уровне верхнего основания колодца. В таком случае изменение потенциальной энергии равно:

\[\Delta {E_п} = 0 — \left( { — mg\frac{{3H}}{4}} \right) = mg\frac{{3H}}{4}\;\;\;\;(4)\]

Насос также сообщает скорость перекачиваемой жидкости. Чтобы её найти, введем понятие расхода воды — отношение всего объема воды ко времени перекачки.

\[Q = \frac{V}{t}\;\;\;\;(5)\]

Представим, что весь объем жидкости \(V\) перекачается в длинный шланг. Тогда этот объём можно записать в виде:

\[V = S \cdot L\]

Площадь поперечного сечения шланга, очевидно, равна:

\[S = \pi {r^2}\]

Тогда формула расхода примет вид:

\[Q = \frac{{\pi {r^2} \cdot L}}{t}\]

Интересно, что если насос качает жидкость равномерно, то отношение \(\frac{L}{t}\) равно искомой скорости жидкости.

\[Q = \pi {r^2} \cdot \upsilon \]

Учитывая (2) и (5), имеем:

\[\pi {r^2} \cdot \upsilon = \frac{{SH}}{{2t}}\]

\[\upsilon = \frac{{SH}}{{2\pi {r^2}t}}\;\;\;\;(6)\]

Изменение кинетической энергии жидкости равно:

\[\Delta {E_к} = \frac{{m{\upsilon ^2}}}{2} — 0 = \frac{{m{\upsilon ^2}}}{2}\;\;\;\;(7)\]

Поставим (4) и (7) в (1):

\[A = mg\frac{{3H}}{4} + \frac{{m{\upsilon ^2}}}{2}\]

\[A = \frac{m}{2}\left( {\frac{{3gH}}{2} + {\upsilon ^2}} \right)\]

Подставим (3) и (6) в последнюю формулу:

\[A = \rho S\frac{H}{4}\left( {\frac{{3gH}}{2} + {{\left( {\frac{{SH}}{{2\pi {r^2}t}}} \right)}^2}} \right)\]

Переведем радиус трубы и время в систему СИ:

\[1,25\; см = \frac{{1,25}}{{100}}\; м = 0,0125\; м\]

\[5\; мин = 5 \cdot 60 \; с = 300\; с\]

Посчитаем ответ:

\[A = 1000 \cdot 0,5 \cdot \frac{5}{4}\left( {\frac{{3 \cdot 10 \cdot 5}}{2} + {{\left( {\frac{{0,5 \cdot 5}}{{2 \cdot 3,14 \cdot {{0,0125}^2} \cdot 300}}} \right)}^2}} \right) = 91952,33\; Дж \approx 92\; кДж\]