Решение: Кран равномерно поднимает груз со скоростью 0,3 м/с и одновременно движется

Условие задачи:

Кран равномерно поднимает груз со скоростью 0,3 м/с и одновременно движется по рельсам со скоростью 0,4 м/с. Чему равна скорость груза относительно Земли?

Задача №1.7.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_1=0,3\) м/с, \(\upsilon_0=0,4\) м/с, \(\upsilon-?\)

Решение задачи:

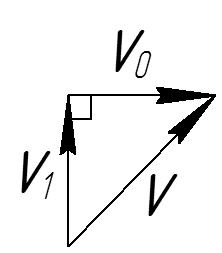Это задача на применение правила сложения скоростей. Сформулируем его применительно к нашей задаче: скорость груза относительно Земли \(\overrightarrow \upsilon\) равна сумме скорости груза относительно крана \(\overrightarrow {{\upsilon _1}}\) и скорости самого крана \(\overrightarrow {{\upsilon _0}}\).

\[\overrightarrow \upsilon = \overrightarrow {{\upsilon _1}} + \overrightarrow {{\upsilon _0}} \]

Так как движение груза относительно крана и движение самого крана взаимно перпендикулярны, то применим теорему Пифагора:

\[{\upsilon ^2} = \upsilon _1^2 + \upsilon _0^2\]

\[\upsilon = \sqrt {\upsilon _1^2 + \upsilon _0^2} \]

Подставим исходные данные задачи и подсчитаем ответ, хотя можно заметить, что стороны получившегося прямоугольного векторного треугольника составляют Пифагорову тройку, поэтому можно сразу назвать ответ 0,5 м/с.

\[\upsilon = \sqrt {{{0,3}^2} + {{0,4}^2}} = 0,5\; м/с = 1,8\; км/ч\]