Условие задачи:

Маленький шарик массой \(m\), закрепленный на нерастяжимой нити в поле силы тяжести, вращается в вертикальной плоскости. В верхней точке траектории натяжение нити равно нулю. Каково натяжение нити в нижней точке траектории?

Задача №2.8.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m\), \(T_1=0\), \(T_2-?\)

Решение задачи:

Основная ошибка, которую совершают большинство тех, кто решает эту задачу — неверно мыслят о том, что скорость шарика одинакова во всех точках его круговой траектории. Видимо они думают, что раз шарик вращается, то вращается с одной угловой, а значит и линейной скоростью. Но это не так!

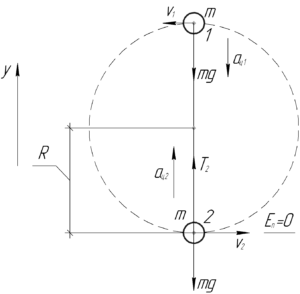
На схеме к рисунку представлены моменты, когда шарик находится в верхней (1) и нижней (2) точках своей траектории. Запишем второй закон Ньютона в проекции на ось \(y\) для этих моментов времени:

\[\left\{ \begin{gathered}
mg + {T_1} = m{a_{ц1}} \;\;\;\;(1)\hfill \\
{T_2} — mg = m{a_{ц2}} \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Заметьте, что так как скорость шарика везде разная, то различаются и центростремительные ускорения.

Сложим эти два выражения, а так как по условию \(T_1=0\), то:

\[{T_2} = m\left( {{a_{ц1}} + {a_{ц2}}} \right)\]

Центростремительное ускорение в общем случае можно найти по формуле:

\[a = \frac{{{\upsilon ^2}}}{R}\]

Здесь \(R\) — длина нити и, в то же время, радиус кривизны траектории движения шарика. Тогда:

\[{T_2} = m\left( {\frac{{\upsilon _1^2}}{R} + \frac{{\upsilon _2^2}}{R}} \right) = \frac{m}{R}\left( {\upsilon _1^2 + \upsilon _2^2} \right)\;\;\;\;(3)\]

Так как отсутствуют неконсервативные силы, то по закону сохранения энергии полная механическая энергия шарика сохраняется. Нуль потенциальной энергии выберем на уровне нижней траектории шарика (точка 2). Тогда очевидно, что в точке 1 имеется кинетическая \(E_{к1}\) и потенциальная энергия \(E_{п1}\), а в точке 2 — только кинетическая \(E_{к2}\).

\[E = const\]

\[{E_{к1}} + {E_{п1}} = {E_{к2}}\]

\[\frac{{m\upsilon _1^2}}{2} + mg \cdot 2R = \frac{{m\upsilon _2^2}}{2}\]

Обратите внимание на то, что в точке 1 шарик находится на высоте \(2R\) от уровня отсчета потенциальной энергии.

\[\upsilon _1^2 + 4gR = \upsilon _2^2\;\;\;\;(4)\]

Из выражения (1) системы следует, что:

\[mg = m{a_1}\]

\[\frac{{\upsilon _1^2}}{R} = g \Rightarrow \upsilon _1^2 = gR\]

Тогда из выражения (4) следует:

\[\upsilon _2^2 = gR + 4gR = 5gR\]

В итоге, подставив все полученное в выражение (3), имеем:

\[{T_2} = \frac{m}{R}\left( {gR + 5gR} \right) = 6mg\]

Ответ: \(6mg\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.13 Камень массой 2 кг брошен вертикально вверх, его начальная кинетическая энергия
2.8.15 Мальчик раскачивается на качелях. При максимальном отклонении от положения
2.8.16 Оконная штора массой 1 кг и длиной 2 м навертывается на валик, расположенный