icodepro.ruУсловие задачи:
Пуля вылетает из ствола под углом 45° к горизонту со скоростью 60 м/с. На каком ближайшем расстоянии, считая по горизонтальному направлению от места выстрела, будет находиться пуля на высоте 50 м?
Задача №1.6.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=45^\circ\), \(v_0=60\) м/с, \(h=50\) м, \(L-?\)
Решение задачи:
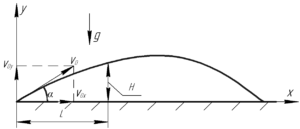Решение данной задачи мы проиллюстрируем рисунком, который приведен справа.
Запишем уравнения движения тела в проекциях на привычные оси \(x\) и \(y\).
\[\left\{ \begin{gathered}
x = {v_0}\cos \alpha \cdot t\;\;\;\;(1) \hfill \\
y = {v_0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2}\;\;\;\;(2) \hfill \\
\end{gathered} \right.\]
Теперь, используя второе записанное уравнение найдем время, за которое тело поднимется на высоту \(h=50\) м. Для этого нам придется решить квадратное уравнение.
\[h = {v_0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2}\]
\[g{t^2} — 2{v_0}\sin \alpha \cdot t + 2h = 0\]
\[D = 4v_0^2{\sin ^2}\alpha — 8gh\]
\[t = \frac{{2{v_0}\sin \alpha \pm \sqrt {4v_0^2{{\sin }^2}\alpha — 8gh} }}{{2g}}\]
Решая данное квадратное уравнение, вполне нормально ожидать два его решения, поскольку тело за все время полета посетит высоту \(h=50\) м два раза: один раз при подъеме и один раз при спуске. Поскольку нам необходимо найти ближайшее расстояние, то очевидно, что оно будет наблюдаться при подъеме, поэтому нас интересует корень, показанный ниже (который со знаком «минус»).
\[t = \frac{{2{v_0}\sin \alpha — \sqrt {4v_0^2{{\sin }^2}\alpha — 8gh} }}{{2g}}\]
Задача практически решена, и я считаю, что нет смысла «тащить» эту формулу дальше, поэтому я подсчитаю ее значение прямо сейчас, подставив исходные данные в формулу в системе СИ.
\[t = \frac{{2 \cdot 60 \cdot \sin 45^\circ — \sqrt {4 \cdot {{60}^2} \cdot {{\sin }^2}45^\circ — 8 \cdot 50 \cdot 10} }}{{2 \cdot 10}} = 1,41\; с.\]
Для того, чтобы получить ответ, подставим это время в уравнение (1).
\[L = {v_0}\cos \alpha \cdot t\]
\[L = 60 \cdot \cos 45^\circ \cdot 1,41 = 59,82\; м.\]
Ответ: 59,82 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.8 Мяч, брошенный со скоростью 10 м/с под углом 45 градусов
1.6.10 Снаряд вылетает из орудия со скоростью 1000 м/с под углом 60
1.6.11 Тело бросили под углом 60 градусов к горизонту со скоростью 10 м/с
Почему проекции начальной скорости показаны векторами? Ведь проекция — всегда скалярная величина!
Это скорее разложение вектора начальной скорости по осям координат. Я не один так делаю, посмотрите книги Касаткиной И.Л. (в новом издании аналогичное изображено прямо на обложке, ха-ха!).
Почему проекция oy и высота h равны в задаче?
Уравнения движения позволяют найти координату тела в любой момент времени, например:\[y = {\upsilon _0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2}\]
Объясняю на примере, пусть \(\tau\) — это время, за которое тело достигнет наивысшей точки своей траектории. Тогда высоту этой точки над Землей \(H\) можно найти из уравнения движения, при этом мы заменяем время \(t\) на \(\tau\), а координату \(y\) на \(H\), то есть: \[H = {\upsilon _0}\sin \alpha \cdot \tau — \frac{{g{\tau ^2}}}{2}\]
Собственно в вышеприведенной задаче все также. Мне нужно найти время, я записываю уравнение движения, вместо \(y\) пишу \(h\), тогда решив квадратное уравнение, я найду время \(t\), за которое тело достигнет этой высоты.
вообще если не считать синусы/косинусы а довести все до конца то получается 60м
Ну мы итак получили результат практически 60 м
Кхем, возможно, мой вопрос покажется глупым, но почему для проекции на ось х используется именно cos? а не sin??
Потому что при проецировании вектора скорости на ось x в получившемся прямоугольном треугольнике искомая проекция является прилежащим катетом — именно поэтому косинус, а не синус.