Решение: Сосуд объемом 5 л разделен перегородкой на две части, заполненные одним газом

Условие задачи:

Сосуд объемом 5 л разделен перегородкой на две части, заполненные одним газом под давлением 80 и 30 кПа. После удаления перегородки в сосуде установилось давление 70 кПа. Определить, какой объем имела часть сосуда с большим давлением.

Задача №4.2.97 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V=5\) л, \(p_1=80\) кПа, \(p_2=30\) кПа, \(p=70\) кПа, \(V_1-?\)

Решение задачи:

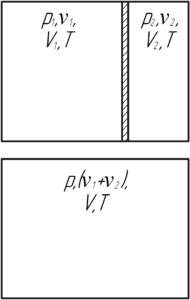Запишем три раза уравнение Клапейрона-Менделеева: для частей газа по обе стороны от перегородки до её удаления и для всего газа после удаления перегородки. Будем считать, что температура газа всегда оставалась неизменной.

\[\left\{ \begin{gathered}
{p_1}{V_1} = {\nu _1}RT \;\;\;\;(1)\hfill \\
{p_2}{V_2} = {\nu _2}RT \;\;\;\;(2)\hfill \\
pV = \left( {{\nu _1} + {\nu _2}} \right)RT \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]

Сложим уравнения (1) и (2), тогда получим:

\[{p_1}{V_1} + {p_2}{V_2} = \left( {{\nu _1} + {\nu _2}} \right)RT\]

Правые части полученного равенства и уравнения (3) равны, поэтому:

\[{p_1}{V_1} + {p_2}{V_2} = pV\]

Очевидно, что сумма объемов \(V_1\) и \(V_2\) равна объему сосуда \(V\):

\[{V_1} + {V_2} = V\]

\[{V_2} = V — {V_1}\]

Тогда имеем:

\[{p_1}{V_1} + {p_2}\left( {V — {V_1}} \right) = pV\]

Осталось только из этого равенства выразить объем \(V_1\), для чего раскроем скобки в левой части:

\[{p_1}{V_1} + {p_2}V — {p_2}{V_1} = pV\]

\[\left( {{p_1} — {p_2}} \right){V_1} = \left( {p — {p_2}} \right)V\]