Условие задачи:
Циклотрон предназначен для ускорения протонов до энергии 5 МэВ. Определить наибольший радиус орбиты, по которой движется протон, если индукция магнитного поля 1 Тл.
Задача №8.2.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(W=5\) МэВ, \(B=1\) Тл, \(R-?\)
Решение задачи:
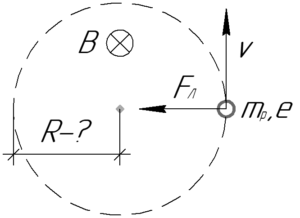 На протон, движущийся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:
На протон, движущийся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:
\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(1)\]
Здесь \(B\) — индукция магнитного поля, \(\upsilon\) — скорость протона, \(e\) — модуль заряда протона, \(\alpha\) — угол между вектором скорости и вектором магнитной индукции (примем равным 90°, так как иного не сказано в условии).
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена влево.
Сила Лоренца \(F_Л\) сообщает протону центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:
\[{F_Л} = {m_p}{a_ц}\;\;\;\;(2)\]
Центростремительное ускорение \(a_ц\) можно определить через скорость \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(3)\]
Подставим (3) в (2), тогда:
\[{F_Л} = \frac{{{m_p}{\upsilon ^2}}}{R}\;\;\;\;(4)\]
Приравняем правые части (1) и (4):
\[B\upsilon e\sin \alpha = \frac{{{m_p}{\upsilon ^2}}}{R}\]
Имеем:
\[Be\sin \alpha = \frac{{{m_p}\upsilon }}{R}\]
\[R = \frac{{{m_p}\upsilon }}{{Be\sin \alpha }}\;\;\;\;(5)\]
Кинетическая энергия протона \(W\) равна:
\[W = \frac{{{m_p}{\upsilon ^2}}}{2}\]
Выразим из этой формулы неизвестную скорость протона \(\upsilon\):
\[\upsilon = \sqrt {\frac{{2W}}{{{m_p}}}} \;\;\;\;(6)\]
Осталось только подставить выражение (6) в формулу (5):
\[R = \frac{{{m_p}}}{{Be\sin \alpha }}\sqrt {\frac{{2W}}{{{m_p}}}} \]
\[R = \frac{{\sqrt {2W{m_p}} }}{{Be\sin \alpha }}\]
Напомним, что масса протона \(m_p\) равна 1,672·10-27 кг, а его заряд \(e\) равен 1,6·10-19 Кл. Также заметим, что 1 эВ равен 1,6·10-19 Дж.Численный ответ равен:
\[R = \frac{{\sqrt {2 \cdot 5 \cdot {{10}^6} \cdot 1,6 \cdot {{10}^{ — 19}} \cdot 1,672 \cdot {{10}^{ — 27}}} }}{{1 \cdot 1,6 \cdot {{10}^{ — 19}} \cdot \sin 90^\circ }} = 0,32\;м\]
Ответ: 0,32 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.2.17 Двухвалентный ион движется со скоростью 481 км/с в однородном магнитном поле
8.2.19 Протон движется в вакууме в однородном магнитном поле с индукцией 94,2 мкТл
8.2.20 Электрон, движущийся со скоростью 10^7 м/с, влетает в однородное магнитное поле

 icodepro.ru
icodepro.ru