Условие задачи:
Во сколько раз уменьшится сила тяготения тела к Земле при удалении его от поверхности Земли на расстояние, равное радиусу Земли?
Задача №2.5.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=R\), \(\frac{F_{т1}}{F_{т2}}-?\)
Решение задачи:
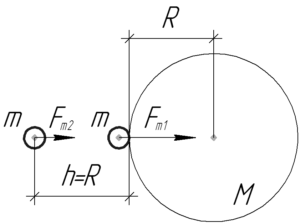 Силу тяготения тела к Земле \(F_{т1}\), когда тело находится на поверхности Земли, найдем из закона всемирного тяготения:
Силу тяготения тела к Земле \(F_{т1}\), когда тело находится на поверхности Земли, найдем из закона всемирного тяготения:
\[{F_{т1}} = G\frac{{Mm}}{{{R^2}}}\]
Здесь \(G\) — гравитационная постоянная, \(M\) — масса Земли, а \(m\) — масса рассматриваемого тела.
Если тело удалить на расстояние \(h\) от поверхности Земли, то сила тяготения \(F_{т2}\) измениться. Тогда:
\[{F_{т2}} = G\frac{{Mm}}{{{{\left( {R + h} \right)}^2}}}\]
Так как по условию \(h=R\), то:
\[{F_{т2}} = G\frac{{Mm}}{{{{\left( {R + R} \right)}^2}}} = G\frac{{Mm}}{{4{R^2}}}\]
В конце концов осталось найти искомое отношение \(\frac{F_{т1}}{F_{т2}}\):
\[\frac{{{F_{т1}}}}{{{F_{т2}}}} = \frac{{GMm \cdot 4{R^2}}}{{{R^2} \cdot GMm}} = 4\]
Ответ: в 4 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.43 В сельском хозяйстве применяются дисковые разбрасыватели удобрений. Какой должна
2.5.2 Определить силу взаимодействия тела массой 2 кг и Земли, если тело удалено от
2.5.3 Во сколько раз ускорение свободного падения около поверхности Земли больше

 icodepro.ru
icodepro.ru