Условие задачи:

Воздушный шар объемом 20 м³, наполненный гелием, поднялся на высоту 180 м за 0,5 минуты. Масса шара с оборудованием и корзиной 12 кг. Найти массу груза, поднятого шаром. Плотности воздуха и гелия при этих высотах считать постоянными и равными 1,29 и 0,18 кг/м³, соответственно.

Задача №4.2.83 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V=20\) м³, \(H=180\) м, \(t=0,5\) мин, \(m_{об}=12\) кг, \(\rho_в=1,29\) кг/м³, \(\rho=0,18\) кг/м³, \(m_{гр}-?\)

Решение задачи:

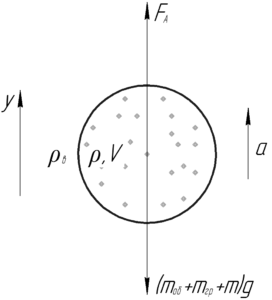Воздушный шар будет двигаться равноускоренно вверх под действием следующих сил: силы Архимеда и силы тяжести шара с оборудованием, грузом и гелием. Запишем второй закон Ньютона в проекции на ось \(y\):

\[{F_А} — \left( {{m_{об}} + {m_{гр}} + m} \right)g = \left( {{m_{об}} + {m_{гр}} + m} \right)a\;\;\;\;(1)\]

Силу Архимеда \(F_А\) определяет по следующей формуле:

\[{F_А} = {\rho _в}gV\]

Тогда равенство (1) станет таким:

\[{\rho _в}gV — \left( {{m_{об}} + {m_{гр}} + m} \right)g = \left( {{m_{об}} + {m_{гр}} + m} \right)a\]

Выразим отсюда искомую массу груза \(m_{гр}\):

\[{\rho _в}gV = \left( {{m_{об}} + {m_{гр}} + m} \right)\left( {a + g} \right)\]

\[\frac{{{\rho _в}gV}}{{a + g}} = \left( {{m_{об}} + {m_{гр}} + m} \right)\]

\[{m_{гр}} = \frac{{{\rho _в}gV}}{{a + g}} — {m_{об}} — m\;\;\;\;(2)\]

Уравнение движения шара вдоль оси \(y\) выглядит так:

\[H = \frac{{a{t^2}}}{2}\]

Тогда ускорение шара \(a\) найдем по формуле:

\[a = \frac{{2H}}{{{t^2}}}\;\;\;\;(3)\]

Массу гелия в шаре \(m\) найдём через его плотность \(\rho\) и объем шара \(V\):

\[m = \rho V\;\;\;\;(4)\]

Формула (2) с учетом выражений (3) и (4) примет вид:

\[{m_{гр}} = \frac{{{\rho _в}gV}}{{\frac{{2H}}{{{t^2}}} + g}} — {m_{об}} — \rho V\]

\[{m_{гр}} = \frac{{{\rho _в}gV{t^2}}}{{2H + g{t^2}}} — {m_{об}} — \rho V\]

Переведём время подъема в систему СИ:

\[0,5\;мин = 30\;с\]

Произведём вычисления:

\[{m_{гр}} = \frac{{1,29 \cdot 10 \cdot 20 \cdot {{30}^2}}}{{2 \cdot 180 + 10 \cdot {{30}^2}}} — 12 — 0,18 \cdot 20 = 9,21\;кг\]

Ответ: 9,21 кг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.82 Два баллона с объемами 20 и 10 л соединены длинной тонкой трубкой и содержат 6 моль
4.2.84 Внутри замкнутого цилиндра, наполненного воздухом, находится шарик радиусом 3 см
4.2.85 На дне цилиндра, наполненного воздухом, плотность которого 1,29 кг/м3, лежит полый