Через невесомый блок перекинута нерастяжимая нить, к одному из концов которой

Условие задачи:

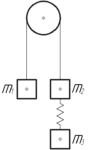Через невесомый блок перекинута нерастяжимая нить, к одному из концов которой привязан груз массой \(m_1=2\) кг. На другом конце закреплены грузы \(m_2=0,3\) кг и \(m_3=0,2\) кг, соединенные пружиной с коэффициентом жесткости \(k=100\) Н/м. Определить растяжение пружины при установившемся движении системы, если массами нити и пружины можно пренебречь.

Задача №2.2.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m_1=2\) кг, \(m_2=0,3\) кг, \(m_3=0,2\) кг, \(k=100\) Н/м, \(x-?\)

Решение задачи:

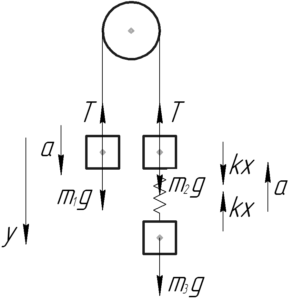На схеме покажем все силы, действующие на каждый груз. Понятно, что груз \(m_1\) будет двигаться вниз, так как он самый тяжелый, а остальные – вверх. У всех грузов при установившемся движении будет одинаковое ускорение \(a\). Запишем второй закон Ньютона в проекции на ось \(y\) для каждого груза:

\[\left\{ \begin{gathered}
{m_1}g – T = {m_1}a \;\;\;\;(1)\hfill \\
{m_2}g + kx – T = – {m_2}a \;\;\;\;(2)\hfill \\
{m_3}g – kx = – {m_3}a \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]

Из равенства (1) вычтем равенство (2) и (3), тогда:

\[{m_1}g – T – {m_2}g – kx + T – {m_3}g + kx = {m_1}a + {m_2}a + {m_3}a\]

\[g\left( {{m_1} – {m_2} – {m_3}} \right) = a\left( {{m_1} + {m_2} + {m_3}} \right)\]

\[a = \frac{{g\left( {{m_1} – {m_2} – {m_3}} \right)}}{{{m_1} + {m_2} + {m_3}}}\]

Из равенства (3) системы выразим деформацию пружины \(x\):

\[x = \frac{{{m_3}}}{k}\left( {g + a} \right)\]

Подставим в эту формулу полученное выражение для ускорения \(a\):

\[x = \frac{{{m_3}}}{k}\left( {g + \frac{{g\left( {{m_1} – {m_2} – {m_3}} \right)}}{{{m_1} + {m_2} + {m_3}}}} \right)\]

Внутри скобок приведем под общий знаменатель и раскроем скобки:

\[x = \frac{{{m_3}}}{k} \cdot \frac{{g\left( {{m_1} + {m_2} + {m_3}} \right) + g\left( {{m_1} – {m_2} – {m_3}} \right)}}{{{m_1} + {m_2} + {m_3}}} = \frac{{{m_3}}}{k} \cdot \frac{{g{m_1} + g{m_2} + g{m_3} + g{m_1} – g{m_2} – g{m_3}}}{{{m_1} + {m_2} + {m_3}}}\]

\[x = \frac{{2g{m_1}{m_3}}}{{k\left( {{m_1} + {m_2} + {m_3}} \right)}}\]

Посчитаем ответ:

\[x = \frac{{2 \cdot 10 \cdot 2 \cdot 0,2}}{{100 \cdot \left( {2 + 0,3 + 0,2} \right)}} = 0,032\; м = 32\; мм\]

Ответ: 32 мм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.2.6 Две гири неравной массы висят на концах нити, перекинутой через невесомый блок
2.2.8 К концам нерастянутой нити, перекинутой через застопоренный блок, подвешенный
2.2.9 К одному концу невесомой и нерастяжимой нити, перекинутой через невесомый блок