Решение: К резинке длиной 50 см привязана гирька массой 20 г. При вращении гирьки

Условие задачи:

К резинке длиной 50 см привязана гирька массой 20 г. При вращении гирьки в горизонтальной плоскости резинка удлинилась на 5 см. Определите линейную скорость гирьки, если жесткость резины 10 Н/м.

Задача №2.6.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(l=50\) см, \(m=20\) г, \(x=5\) см, \(k=10\) Н/м, \(\upsilon-?\)

Решение задачи:

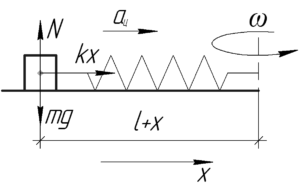На гирьку действуют три силы: сила тяжести \(mg\), сила реакции опоры \(N\) и сила упругости \(kx\). Понятно, что по оси \(x\) действует только сила упругости, которая сообщает гирьке центростремительное ускорение. Применим второй закон Ньютона в проекции на ось \(x\):

\[kx = m{a_ц}\;\;\;\;(1)\]

Если при вращении резинка деформирована на величину \(x\), значит гирька находится на расстоянии \(\left( {l + x} \right)\) от оси вращения. Поэтому центростремительное ускорение \(a_ц\) можно найти по такой формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{{l + x}}\]

Здесь \(\upsilon\) – это искомая скорость. Тогда равенство (1) преобразуется в такой вид:

\[kx = \frac{{m{\upsilon ^2}}}{{l + x}}\]

\[\upsilon = \sqrt {\frac{{kx\left( {l + x} \right)}}{m}} \]

Переводим длину и деформацию резинки, а также массу гирьки в систему СИ:

\[50\;см = \frac{{50}}{{100}}\;м = 0,5\;м\]

\[5\;см = \frac{{5}}{{100}}\;м = 0,05\;м\]

\[20\;г = \frac{{20}}{{1000}}\;кг = 0,02\;кг\]

\[\upsilon = \sqrt {\frac{{10 \cdot 0,05 \cdot \left( {0,5 + 0,05} \right)}}{{0,02}}} = 3,71\;м/с = 13,35\;км/ч\]