Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг

Условие задачи:

Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг с ребром 0,2 м с грани на ребро?

Задача №2.8.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) кг, \(a=0,2\) м, \(A-?\)

Решение задачи:

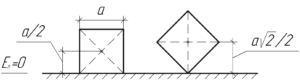Понятно, что когда куб поставят с грани на ребро, то у него измениться потенциальная энергия, поскольку центр масс куба станет расположен немного выше. Вообще, центр масс куба располагается в точке пересечения его диагоналей. То есть на схеме, приведенной к задаче, где мы изобразили вид куба спереди, проекция центра масс будет находиться на пересечении диагоналей грани куба.

Работа внешней силы равна изменению потенциальной энергии куба.

\[A = \Delta E_п = {E_2} – {E_1}\]

Если взять уровень нуля потенциальной энергии на поверхности, то центр масс расположен на высоте \(\frac{a}{2}\) от него, а значит начальная потенциальная энергия равна:

\[E_1 = mg\frac{a}{2}\]

Когда куб поставят на ребро, то центр масс будет уже находиться на высоте \(\frac{{a\sqrt 2 }}{2}\), так как длина диагонали грани куба равна \(a\sqrt 2\) по теореме Пифагора, то есть:

\[E_2 = mg\frac{{a\sqrt 2 }}{2}\]

В итоге:

\[A = mg\frac{{a\sqrt 2 }}{2} – mg\frac{a}{2} = mg\frac{a}{2}\left( {\sqrt 2  – 1} \right)\]

Посчитаем численный ответ:

\[A = 10 \cdot 10 \cdot \frac{{0,2}}{2}\left( {\sqrt 2  – 1} \right) = 4,14\; Дж\]

Ответ: 4,14 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.27 Для откачки воды из шахты глубиной 20 м поставлен насос с двигателем мощностью
2.8.29 Камень бросили под углом 60 градусов к горизонту со скоростью 15 м/с. Найдите
2.8.30 На нити длиной 1 м подвешено тело массой 1 кг. На какой максимальный угол