Условие задачи:
Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе двух свинцовых шаров массой 1 кг каждый, скользящих без вращения по абсолютно гладкой поверхности. До удара шары двигались по одной прямой в одном направлении. Скорость первого шара равна 10 см/с, скорость второго — 20 см/с.
Задача №2.10.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=1\) кг, \(\upsilon_1=10\) см/с, \(\upsilon_2=20\) см/с, \(Q-?\)
Решение задачи:
- закон сохранения импульса (ЗСИ) в проекции на ось \(x\), поскольку система, состоящая из двух шаров замкнута в этом направлении;
- закон сохранения энергии (ЗСЭ), но учтем, что часть начальной кинетической энергии шаров при абсолютно неупругом ударе переходит в теплоту \(Q\).
\[\left\{ \begin{gathered}
m{\upsilon _1} + m{\upsilon _2} = 2mu \hfill \\
\frac{{m\upsilon _1^2}}{2} + \frac{{m\upsilon _2^2}}{2} = \frac{{2m{u^2}}}{2} + Q \hfill \\
\end{gathered} \right.\]
Из ЗСИ выразим скорость шаров после удара:
\[u = \frac{{{\upsilon _1} + {\upsilon _2}}}{2}\]
Полученное выражение подставим в ЗСЭ:
\[\frac{{m\upsilon _1^2}}{2} + \frac{{m\upsilon _2^2}}{2} = \frac{{2m}}{2}{\left( {\frac{{{\upsilon _1} + {\upsilon _2}}}{2}} \right)^2} + Q\]
Раскроем квадрат суммы в правой части уравнения:
\[\frac{{m\upsilon _1^2}}{2} + \frac{{m\upsilon _2^2}}{2} = \frac{{2m}}{2}\left( {\frac{{\upsilon _1^2 + 2{\upsilon _1}{\upsilon _2} + \upsilon _2^2}}{4}} \right) + Q\]
Откроем скобки:
\[\frac{{m\upsilon _1^2}}{2} + \frac{{m\upsilon _2^2}}{2} = \frac{{m\upsilon _1^2}}{4} + \frac{{m{\upsilon _1}{\upsilon _2}}}{2} + \frac{{m\upsilon _2^2}}{4} + Q\]
\[Q = \frac{{m\upsilon _1^2}}{4} — \frac{{m{\upsilon _1}{\upsilon _2}}}{2} + \frac{{m\upsilon _2^2}}{4} = \frac{m}{4}\left( {\upsilon _1^2 — 2{\upsilon _1}{\upsilon _2} + \upsilon _2^2} \right)\]
\[Q = \frac{m}{4}{\left( {{\upsilon _1} — {\upsilon _2}} \right)^2}\]
Получилась «красивая» формула для расчета ответа. Переведем скорости в единицы системы СИ.
\[10\; см/с = \frac{{10}}{{100}}\; м/с = 0,1\; м/с\]
\[20\; см/с = \frac{{20}}{{100}}\; м/с = 0,2\; м/с\]
Считаем ответ:
\[Q = \frac{1}{4}{\left( {0,1 — 0,2} \right)^2} = 2,5 \cdot 10^{-3}\; Дж = 2,5\; мДж\]
Ответ: 2,5 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с

 icodepro.ru
icodepro.ru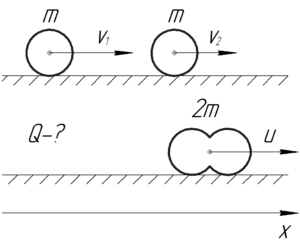
Разве не 2,5 мДж = 2,5 * 106 Дж?
Вы путаете приставку «милли» (10-3, пишется маленькая «м») с приставкой «мега» (106, пишется большая «М»).