Условие задачи:
Два одинаковых маленьких шарика, имеющих одинаковые заряды 2 мкКл, соединены пружиной. Шарики колеблются так, что расстояние между ними меняется от 10 до 40 см. Найти жесткость пружины, если её длина в свободном состоянии равна 20 см.
Задача №6.3.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q=2\) мкКл, \(l_1=10\) см, \(l_2=40\) см, \(l=20\) см, \(k_{пр}-?\)
Решение задачи:
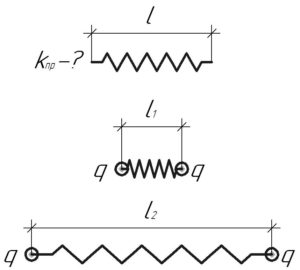 Очевидно, что максимальная деформация пружины будет равна \(\left( {{l_2} — l} \right)\), а минимальная — \(\left( {l — {l_1}} \right)\).
Очевидно, что максимальная деформация пружины будет равна \(\left( {{l_2} — l} \right)\), а минимальная — \(\left( {l — {l_1}} \right)\).
Энергия системы «пружина — шарики» состоит из потенциальной энергии деформации пружины, потенциальной энергии взаимодействия зарядов шариков и кинетической энергии шариков. Запишем закон сохранения для указанной системы для крайних положений, т.е. в которых скорость (а значит и кинетическая энергия) шариков равна нулю.
\[\frac{{k{q^2}}}{{{l_2}}} + \frac{{{k_{пр}}{{\left( {{l_2} — l} \right)}^2}}}{2} = \frac{{k{q^2}}}{{{l_1}}} + \frac{{{k_{пр}}{{\left( {l — {l_1}} \right)}^2}}}{2}\]
Здесь \(k\) — коэффициент пропорциональности (в законе Кулона), равный 9·109 Н·м2/Кл2, а \(k_{пр}\) — искомая жесткость пружины.
Сгруппируем в левой части потенциальные энергии пружины, а в правой — потенциальные энергии взаимодействия зарядов:
\[\frac{{{k_{пр}}}}{2}\left( {{{\left( {{l_2} — l} \right)}^2} — {{\left( {l — {l_1}} \right)}^2}} \right) = \frac{{k{q^2}}}{{{l_1}}} — \frac{{k{q^2}}}{{{l_2}}}\]
В левой части в скобках распишем разность квадратов, в правой приведём под общий знаменатель:
\[\frac{{{k_{пр}}}}{2}\left( {{l_2} — l — l + {l_1}} \right)\left( {{l_2} — l + l — {l_1}} \right) = \frac{{k{q^2}\left( {{l_2} — {l_1}} \right)}}{{{l_1}{l_2}}}\]
\[\frac{{{k_{пр}}}}{2}\left( {{l_1} + {l_2} — 2l} \right)\left( {{l_2} — {l_1}} \right) = \frac{{k{q^2}\left( {{l_2} — {l_1}} \right)}}{{{l_1}{l_2}}}\]
\[\frac{{{k_{пр}}}}{2}\left( {{l_1} + {l_2} — 2l} \right) = \frac{{k{q^2}}}{{{l_1}{l_2}}}\]
В итоге мы с Вами получим такое решение задачи в общем виде:
\[{k_{пр}} = \frac{{2k{q^2}}}{{{l_1}{l_2}\left( {{l_1} + {l_2} — 2l} \right)}}\]
Осталось только посчитать численный ответ:
\[{k_{пр}} = \frac{{2 \cdot 9 \cdot {{10}^9} \cdot {{\left( {2 \cdot {{10}^{ — 6}}} \right)}^2}}}{{0,1 \cdot 0,4 \cdot \left( {0,1 + 0,4 — 2 \cdot 0,2} \right)}} = 18\;Н/м\]
Ответ: 18 Н/м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.28 На сколько изменится потенциальная энергия взаимодействия зарядов 25 и -4 нКл
6.3.30 На расстоянии 90 см от поверхности шара радиусом 10 см, несущего положительный
6.3.31 Электрон переместился из точки с потенциалом 200 В в точку с потенциалом 300 В

 icodepro.ru
icodepro.ru
как вы так дробь раскрыли
Невозможно прочитать!!!!!!!!!!!!!!!!!!!! ??f
rac{{{k_{пр}}}}{2}\left( {{l_1} + {l_2} – 2l} \right)\left( {{l_2} – {l_1}} \right) = \frac{{k{q^2}\left( {{l_2} – {l_1}} \right)}}{{{l_1}{l_2}}}\]
\[\frac{{{k_{пр}}}}{2}\left( {{l_1}
ВОТ ЭТО ПОКАЗЫВАЕТ