Решение: Два одинаковых точечных заряда по 5 мкКл взаимодействуют с силой 10 Н

Условие задачи:

Два одинаковых точечных заряда по 5 мкКл взаимодействуют с силой 10 Н в вакууме. Найти потенциал в центре отрезка, соединяющего эти заряды.

Задача №6.3.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q=5\) мкКл, \(F=10\) Н, \(r=\frac{l}{2}\), \(\varphi-?\)

Решение задачи:

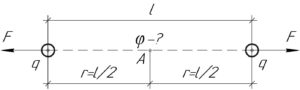Потенциал — это скалярная величина, поэтому искомый потенциал \(\varphi\) (результирующего поля двух зарядов) равен сумме потенциалов электрических полей, создаваемых каждым зарядом, в указанной точке (точке A, смотрите схему). Поэтому:

\[\varphi = \frac{{kq}}{r} + \frac{{kq}}{r}\]

\[\varphi = \frac{{2kq}}{r}\]

Коэффициент пропорциональности \(k\) равен 9·10⁹ Н·м²/Кл².

Так ка точка A находится посередине отрезка, соединяющего заряды, то есть \(r=\frac{l}{2}\), то:

\[\varphi = \frac{{4kq}}{l}\;\;\;\;(1)\]

По условию нам известна сила \(F\), с которой заряды отталкиваются друг от друга (так как они одноимённые). По закону Кулона её можно найти по формуле:

\[F = \frac{{k{q^2}}}{{{l^2}}}\]

Отсюда мы можем выразить неизвестное расстояние между зарядами \(l\):

\[l = q\sqrt {\frac{k}{F}}\;\;\;\;(2)\]

Подставим (2) в (1), тогда получим:

\[\varphi = \frac{{4kq}}{q}\sqrt {\frac{F}{k}} \]

\[\varphi = 4\sqrt {kF} \]

Произведём расчёт численного ответа этой задачи:

\[\varphi = 4\sqrt {9 \cdot {{10}^9} \cdot 10} = 12 \cdot {10^5}\;В = 1200\;кВ\]