icodepro.ruУсловие задачи:
Два шарика массой по 1 г подвешены на нитях длиной 0,5 м в одной точке. После сообщения им отрицательного заряда угол между нитями стал 60°. Чему равна электрическая сила их взаимодействия?
Задача №6.1.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=1\) г, \(l=0,5\) м, \(\alpha=60^\circ\), \(F_{эл}-?\)
Решение задачи:
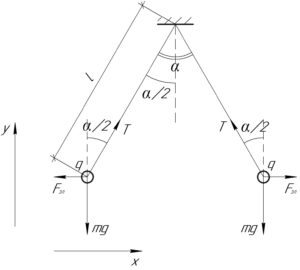После сообщения каждому их шариков отрицательного заряда они разойдутся на угол \(\alpha\) (как показано на рисунке), при этом в какой-то момент времени шарики придут в равновесие. В этом состоянии на каждый шарик действуют три силы: сила тяжести \(mg\), искомая кулоновская сила отталкивания \(F_{эл}\) и сила натяжения нити \(T\). Запишем первый закон Ньютона в проекции на обе оси координат:
\[\left\{ \begin{gathered}
T \cdot \sin \frac{\alpha }{2} = {F_{эл}} \hfill \\
T \cdot \cos \frac{\alpha }{2} = mg \hfill \\
\end{gathered} \right.\]
Поделим верхнее равенство на нижнее, тогда получим следующее:
\[tg\frac{\alpha }{2} = \frac{{{F_{эл}}}}{{mg}}\]
Откуда мы уже получим решение задачи в общем виде:
\[{F_{эл}} = mg \cdot tg\frac{\alpha }{2}\]
Посчитаем численный ответ к задаче:
\[{F_{эл}} = 0,001 \cdot 10 \cdot tg\frac{{60^\circ }}{2} = 5,8 \cdot {10^{ — 3}}\;Н = 5,8\;мН\]
Ответ: 5,8 мН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.1.25 Два одинаковых шарика подвешены на нитях в воздухе так, что их поверхности
6.1.27 Два маленьких проводящих шарика подвешены на длинных непроводящих нитях
6.1.28 Два одинаковых шарика, имеющих одинаковые заряды 1,6 мкКл, подвешены на одной
У меня задача на подобии, два одинаково заряженных шарика подвешены в воздухе на нитях, закреплены в общей точке. Определить угол между нитями, если заряд каждого шарика равен 5*10^-8 Кл, масса 16 мг, длина каждой нити 50 см. Хелп, не могу посчитать угол, получается tg(x) *sin^2(x)
В Вашем случае я бы решал также, то есть записал бы проекции первого закона Ньютона на обе оси, получил бы:\[\left\{ \begin{gathered}
T\cos \alpha = mg \hfill \\
T\sin \alpha = \frac{{k{q^2}}}{{4{r^2}}} \hfill \\
\end{gathered} \right.\]Тогда, при делении верхнего равенства на нижнее, имеем:\[ctg\alpha = \frac{{4mg{r^2}}}{{k{q^2}}}\]Также из рисунка видно, что:\[ctg\alpha = \frac{{\sqrt {{l^2} — {r^2}} }}{r}\]Тогда:\[\frac{{\sqrt {{l^2} — {r^2}} }}{r} = \frac{{4mg{r^2}}}{{k{q^2}}}\]Возводим в квадрат обе части уравнения:\[\frac{{{l^2} — {r^2}}}{{{r^2}}} = \frac{{16{m^2}{g^2}{r^4}}}{{{k^2}{q^4}}}\]Перемножаем крест-накрест:\[{k^2}{q^4}{l^2} — {k^2}{q^4}{r^2} = 16{m^2}{g^2}{r^6}\]Считаем численные значения коэффициентов перед неизвестной \(r\), тогда получим такое уравнение:\[4,096 \cdot {10^{ — 7}}{r^6} + 5,0625 \cdot {10^{ — 10}}{r^2} — 1,265625 \cdot {10^{ — 10}} = 0\]Если решить это уравнение в каком-нибудь онлайн-сервисе (например, в Wolfram Alpha смотри по ссылке), то один из корней приближенно равен 0,25 м. Тогда \(\alpha=30^\circ\), поскольку катет, лежащий против угла в 30°, равен половине гипотенузы, а искомый угол равен 60°.
Если Вы сможете решить тригонометрическое уравнение, которое получилось у Вас, то пожалуйста скиньте мне решение в личку группы ВК, если Вам нетрудно.
А откуда вы взяли 4 в системе во 2ом уравнение?
У меня \(r\) — расстояние от заряда до вертикали, проведенной из точки подвеса нити. Поэтому расстояние между зарядами у меня равно \(2r\), а если возводить в квадрат, как того требует закон Кулона, то получим \(4r^2\).
Почему tg( alpha / 2 ) = 5,8 ?
Ведь alpha = 60 градусов
60 градусов = pi/3
( pi/3 ) / 2 = pi/6
tan ( pi/6 ) = 0,577 радиан
Тангенс угла — это число, так что в последней строке «радиан» Вы пишите не верно.
Я не утверждал, что \(tg \frac{\alpha}{2} = 5,8\). Перед тангенсом ещё есть два множителя, это 0,001 и 10. Первый из них даст приставку «милли» в ответе, а вот произведение второго с результатом расчета тангенса дает как раз 5,8, поэтому тангенс я, как и Вы, сосчитал правильно.