Решение: Два заряженных шарика с зарядами 300 и 200 нКл, массы которых 0,2 и 0,8 г

Условие задачи:

Два заряженных шарика с зарядами 300 и 200 нКл, массы которых 0,2 и 0,8 г, соединены легкой непроводящей нитью длиной 20 см и движутся вдоль силовой линии однородного поля напряженностью 10 кВ/м. Вектор напряженности электрического поля направлен вертикально вниз. Определить ускорение шариков.

Задача №6.2.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q_1=300\) нКл, \(q_2=200\) нКл, \(m_1=0,2\) г, \(m_2=0,8\) г, \(l=20\) см, \(E=10\) кВ/м, \(a-?\)

Решение задачи:

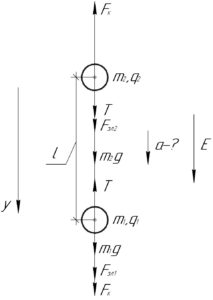На каждый заряженный шарик действует сила тяжести \(mg\), кулоновская сила отталкивания со стороны другого заряда \(F_{к}\), сила натяжения нити \(T\) и сила электрического взаимодействия со стороны электрического поля \(F_{эл1}\) (или \(F_{эл2}\)) (смотрите схему). Оба шарика движутся с ускорением \(a\) вертикально вниз, запишем второй закон Ньютона в проекции на ось \(y\):

\[\left\{ \begin{gathered}
{m_1}g + {F_{к}} – T + {F_{эл1}} = {m_1}a \hfill \\
{m_2}g – {F_{к}} + T + {F_{эл2}} = {m_2}a \hfill \\
\end{gathered} \right.\]

Сложим оба равенства, тогда получим:

\[\left( {{m_1} + {m_2}} \right)g + {F_{эл1}} + {F_{эл2}} = \left( {{m_1} + {m_2}} \right)a\;\;\;\;(1)\]

Люди, хорошо знающие физику, заметят, что фактически мы получили запись теоремы о движении центра масс для системы зарядов.

Силы \(F_{эл1}\) и \(F_{эл2}\), действующие на шарики с зарядами \(q_1\) и \(q_2\) со стороны электрического поля напряженностью \(E\), определим по формулам:

\[\left\{ \begin{gathered}
{F_{эл1}} = E{q_1} \hfill \\
{F_{эл2}} = E{q_2} \hfill \\
\end{gathered} \right.\]

В таком случае равенство (1) примет вид:

\[\left( {{m_1} + {m_2}} \right)g + E{q_1} + E{q_2} = \left( {{m_1} + {m_2}} \right)a\]

\[\left( {{m_1} + {m_2}} \right)g + E\left( {{q_1} + {q_2}} \right) = \left( {{m_1} + {m_2}} \right)a\]

В итоге получим такое решение задачи:

\[a = g + \frac{{E\left( {{q_1} + {q_2}} \right)}}{{{m_1} + {m_2}}}\]

Произведём расчёты:

\[a = 10 + \frac{{10 \cdot {{10}^3} \cdot \left( {300 \cdot {{10}^{ – 9}} + 200 \cdot {{10}^{ – 9}}} \right)}}{{0,2 \cdot {{10}^{ – 3}} + 0,8 \cdot {{10}^{ – 3}}}} = 15\;м/с^2\]