icodepro.ruУсловие задачи:
На нити подвешен маленький шарик массой 10 г, которому сообщили заряд 1 мкКл. Когда к нему поднесли снизу заряженный таким же зарядом шарик, сила натяжения нити уменьшилась в четыре раза. Определить расстояние между центрами шариков.
Задача №6.1.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=10\) г, \(q=1\) мкКл, \(T=\frac{T_0}{4}\), \(R-?\)
Решение задачи:
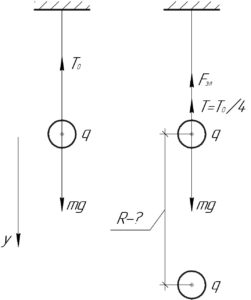В начале шарик с зарядом \(q\) и массой \(m\) находился в равновесии под действием силы тяжести \(mg\) и силы натяжения нити \(T_0\). Запишем первый закон Ньютона в проекции на ось \(y\):
\[mg — {T_0} = 0\;\;\;\;(1)\]
Когда снизу поднесут заряженный таким же зарядом \(q\) другой шарик, то сила натяжения нити уменьшится, поскольку на шарик станет действовать ещё одна сила — сила кулоновского отталкивания \(F_{эл}\). Ещё раз запишем первый закон Ньютона в проекции на ось \(y\):
\[mg — T — {F_{эл}} = 0\]
В условии сказано, что сила натяжения нити уменьшилась в четыре раза, то есть \(T=\frac{T_0}{4}\), поэтому:
\[mg — \frac{{{T_0}}}{4} — {F_{эл}} = 0\]
Умножим и левую, и правую часть этого уравнения на 4, тогда:
\[4mg — {T_0} — 4{F_{эл}} = 0\;\;\;\;(2)\]
Из (2) вычтем (1):
\[3mg = 4{F_{эл}}\]
По закону Кулона два одинаковых заряда \(q\), находящиеся на расстоянии \(R\) друг от друга отталкиваются с силой \(F_{эл}\), которую можно определить по формуле:
\[{F_{эл}} = \frac{{k{q^2}}}{{{R^2}}}\]
В этой формуле \(k\) — коэффициент пропорциональности, равный 9·109 Н·м2/Кл2.
В таком случае имеем:
\[3mg = \frac{{4k{q^2}}}{{{R^2}}}\]
Откуда искомое расстояние между центрами шариков \(R\) можно найти по формуле:
\[R = q\sqrt {\frac{{4k}}{{3mg}}} \]
Произведём расчёт численного ответа:
\[R = 1 \cdot {10^{ — 6}} \cdot \sqrt {\frac{{4 \cdot 9 \cdot {{10}^9}}}{{3 \cdot 0,01 \cdot 10}}} = 0,346\;м\]
Ответ: 0,346 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.1.20 На нити подвешен заряженный шар массой 300 г. Когда к нему поднесли снизу
6.1.22 Три одинаковых точечных заряда по -1,7 нКл каждый находятся в вершинах
6.1.23 Две частицы массой 10 г и зарядом 2 мкКл находятся в вершинах равностороннего
Для решения этой задачи нужно использовать закон Кулона и второй закон Ньютона.
Сначала рассмотрим силу натяжения нити до приближения второго шарика. Она равна весу подвешенного шарика:
T1 = mg,
где m = 10 г = 0.01 кг — масса шарика,
g ? 9.8 м/с2 — ускорение свободного падения.
Тогда T1 = 0.01 кг * 9.8 м/с2 = 0.098 Н.
Когда к шарику поднесли второй заряженный шарик, сила натяжения нити уменьшилась в четыре раза, значит:
T2 = T1 / 4 = 0.098 Н / 4 = 0.0245 Н.
Сила, с которой действует второй шарик на первый, будет равна разности исходной и конечной силы натяжения:
F = T1 — T2 = 0.098 Н — 0.0245 Н = 0.0735 Н.
Согласно закону Кулона, эта сила равна:
F = k * (q1 * q2) / r2,
где k = 8.99 * 10^9 Н*м2/Кл2 — постоянная Кулона,
q1 = q2 = 1 мкКл = 1 * 10^-6 Кл — заряды шариков,
r — искомое расстояние между шариками.
Отсюда получаем:
r = sqrt((k * q1 * q2) / F).
Подставляем известные значения и получаем:
r = sqrt((8.99 * 10^9 Н*м2/Кл2 * (1 * 10^-6 Кл)^2) / 0.0735 Н) ? 0.036 м.
Таким образом, расстояние между центрами шариков составляет примерно 0.036 метра или 3.6 см.
Сначала мы должны установить, что сила тяжести (Fg) остается неизменной. Она определяется по формуле:
Fg = m * g,
где m — масса шарика (10 г = 0.01 кг), а g — ускорение свободного падения (примерно 9.8 м/с^2).
Таким образом, сила тяжести составляет:
Fg = 0.01 кг * 9.8 м/с^2 = 0.098 Н.
Из условия задачи мы знаем, что сила натяжения уменьшилась в четыре раза, когда к шарику поднесли заряженный шарик. Это значит, что сила взаимодействия двух заряженных шариков (Fe) составляет разность между исходной силой тяжести и силой натяжения нити после поднесения второго шарика. С учетом того, что сила натяжения уменьшилась в 4 раза, мы получаем:
Fe = Fg — Fg / 4 = 0.098 Н — 0.098 Н / 4 = 0.0735 Н.
Сила взаимодействия двух зарядов определяется формулой Кулона:
Fe = k * (q1 * q2) / r^2,
где k — постоянная Кулона (9 * 10^9 Н*м^2/Кл^2), q1 и q2 — заряды шариков (1 мкКл = 10^-6 Кл), а r — расстояние между шариками.
Из этой формулы мы можем выразить r:
r = sqrt(k * (q1 * q2) / Fe) = sqrt((9 * 10^9 Н*м^2/Кл^2 * (10^-6 Кл)^2) / 0.0735 Н) ? 0.036 м.
Таким образом, расстояние между центрами шариков составляет примерно 0.036 метра, или 3.6 сантиметра.