Условие задачи:
По тонкому проволочному кольцу радиуса 3 см равномерно распределен заряд 10-9 Кл. Определить разность потенциалов между центром кольца и точкой, находящейся на оси кольца на расстоянии 4 см от центра.
Задача №6.3.60 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R=3\) см, \(Q=10^{-9}\) Кл, \(L=4\) см, \(\Delta \varphi — ?\)
Решение задачи:
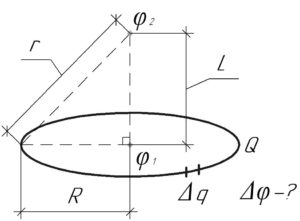 Поскольку заряд \(Q\) распределен равномерно по кольцу, а не сосредоточен в точке, то задачу будем решать следующим образом. Разобьём кольцо на \(N\) одинаковых частей, причём \(N\) — достаточно большое число. Тогда каждая часть будет содержать некоторый точечный заряд \(\Delta q_i\), причем, очевидно, что сумма всех этих точечных зарядов равна \(Q\), то есть справедливо следующее:
Поскольку заряд \(Q\) распределен равномерно по кольцу, а не сосредоточен в точке, то задачу будем решать следующим образом. Разобьём кольцо на \(N\) одинаковых частей, причём \(N\) — достаточно большое число. Тогда каждая часть будет содержать некоторый точечный заряд \(\Delta q_i\), причем, очевидно, что сумма всех этих точечных зарядов равна \(Q\), то есть справедливо следующее:
\[Q = \sum\limits_{i = 1}^N {\Delta {q_i}} \;\;\;\;(1)\]
Каждый такой точечный заряд будет создавать в центре кольца потенциал \(\varphi_{i1}\), который можно найти по формуле:
\[{\varphi _{i1}} = \frac{{k\Delta {q_i}}}{R}\;\;\;\;(2)\]
Так как потенциал — величина скалярная, то потенциал \(\varphi_{1}\) в центре кольца, создаваемый всем зарядом \(Q\), распределённым по кольцу, будем искать по формуле:
\[{\varphi _1} = \sum\limits_{i = 1}^N {{\varphi _{i1}}} \]
Принимая во внимание формулу (2), имеем:
\[{\varphi _1} = \sum\limits_{i = 1}^N {\frac{{k\Delta {q_i}}}{R}} = \frac{k}{R}\sum\limits_{i = 1}^N {\Delta {q_i}} \]
Учитывая (1), получим:
\[{\varphi _1} = \frac{{kQ}}{R}\]
В принципе, выполнив аналогичные рассуждения, Вы можете найти потенциал \(\varphi_{2}\) в точке, находящейся на оси кольца на расстоянии \(L\) от центра. Разница лишь в том, что теперь каждый точечный заряд \(\Delta q_i\) будет находиться от точки, в которой нужно найти потенциал, на неком расстоянии \(r\), которое можно определить по теореме Пифагора (смотрите схему):
\[r = \sqrt {{L^2} + {R^2}} \]
Тогда:
\[{\varphi _2} = \frac{{kQ}}{r}\]
\[{\varphi _2} = \frac{{kQ}}{{\sqrt {{L^2} + {R^2}} }}\]
В итоге искомую разность потенциалов \(\Delta \varphi\) можно найти так:
\[\Delta \varphi = {\varphi _1} — {\varphi _2}\]
\[\Delta \varphi = \frac{{kQ}}{R} — \frac{{kQ}}{{\sqrt {{L^2} + {R^2}} }}\]
\[\Delta \varphi = \frac{{kQ\left( {\sqrt {{L^2} + {R^2}} — R} \right)}}{{R\sqrt {{L^2} + {R^2}} }}\]
Посчитаем численный ответ (при подстановке значений величин в формулу не забывайте переводить их в систему СИ):
\[\Delta \varphi = \frac{{9 \cdot {{10}^9} \cdot {{10}^{ — 9}} \cdot \left( {\sqrt {{{0,04}^2} + {{0,03}^2}} — 0,03} \right)}}{{0,03 \cdot \sqrt {{{0,04}^2} + {{0,03}^2}} }} = 120\;В\]
Ответ: 120 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.59 Внутри шарового металлического слоя, внутренний и внешний радиусы которого
6.3.61 Какую работу необходимо совершить, чтобы три одинаковых точечных положительных
6.3.62 В центре закрепленной полусферы радиуса R, заряженной равномерно с поверхностной

 icodepro.ru
icodepro.ru