Три одинаковых точечных заряда по -1,7 нКл каждый находятся в вершинах

Условие задачи:

Три одинаковых точечных заряда по -1,7 нКл каждый находятся в вершинах равностороннего треугольника. Найти величину точечного заряда, который надо поместить в центре треугольника, чтобы вся система находилась в равновесии?

Задача №6.1.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q=-1,7\) нКл, \(Q-?\)

Решение задачи:

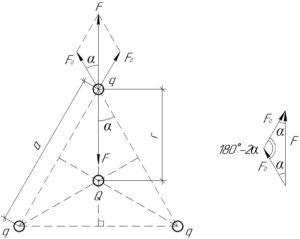Каждый заряд \(q\) действует на другой такой же заряд с силой отталкивания \(F_0\), которую можно определить из закона Кулона:

\[{F_0} = \frac{{k{{\left| q \right|}^2}}}{{{a^2}}}\;\;\;\;(1)\]

Коэффициент пропорциональности \(k\) равен 9·10⁹ Н·м²/Кл².

Теперь найдём равнодействующую двух сил \(F\), с которой два заряда действуют на третий. Для этого воспользуемся принципом независимости действия сил (принципом суперпозиции) и теоремой косинусов (смотри схему к решению).

\[{F^2} = F_0^2 + F_0^2 – 2F_0^2 \cdot \cos \left( {180^\circ – 2\alpha } \right)\]

Из тригонометрии известно, что:

\[\cos \left( {180^\circ – 2\alpha } \right) = – \cos 2\alpha \]

Тогда:

\[{F^2} = F_0^2 + F_0^2 + 2F_0^2 \cdot \cos 2\alpha \]

Также в равностороннем треугольнике угол \(\alpha\) равен 30°, поэтому:

\[{F^2} = F_0^2 + F_0^2 + 2F_0^2 \cdot \cos 60^\circ = 3F_0^2\]

\[F = \sqrt 3 {F_0}\]

Учитывая (1), имеем:

\[F = \frac{{\sqrt 3 k{{\left| q \right|}^2}}}{{{a^2}}}\;\;\;\;(2)\]

Помещенный в центр равностороннего треугольника заряд должен быть положительным, чтобы уравновесить силу \(F\), при этом силу притяжения можно также найти из закона Кулона:

\[F = \frac{{kQ\left| q \right|}}{{{r^2}}}\]

Здесь \(r\) – расстояние от вершины равностороннего треугольника до его центра (центр – это точка пересечения медиан треугольника), его можно найти по такой формуле (за выводом формулы обратитесь к учебнику по математике):

\[r = \frac{{\sqrt 3 a}}{3}\]

В таком случае:

\[F = \frac{{3kQ\left| q \right|}}{{{a^2}}}\;\;\;\;(3)\]

Осталось только приравнять (2) и (3):

\[Q = \frac{{\left| q \right|}}{{\sqrt 3 }}\]

Посчитаем ответ к задаче:

\[Q = \frac{{1,7 \cdot {{10}^{ – 9}}}}{{\sqrt 3 }} = 9,8 \cdot {10^{ – 10}}\;Кл \approx 1\;нКл\]

Ответ: 1 нКл.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.1.21 На нити подвешен маленький шарик массой 10 г, которому сообщили заряд 1 мкКл
6.1.23 Две частицы массой 10 г и зарядом 2 мкКл находятся в вершинах равностороннего
6.1.24 В вертикальной трубке, заполненной воздухом, закреплен точечный заряд 5 мкКл